ある通貨に於ける効率的な金種構成

島崎崇

（1）金額の計算しやすさ

硬貨、紙幣という形態の金は、最近ますます電子マネーに取って代わられている。しかし、人間社会に現金というものが存在する限り、それは皆にとって可能な限り使いやすい方が良い。例えば、硬貨と紙幣は、扱いやすくあるために、適度な大きさと形状でなければならない。又、計算が容易になるように、金種の額面が適切な金額を表すことも重要である。仮に、額面金額が奇妙な金額に設定されていると、金額の計算が煩雑になり、人々は、唯無駄に時間を費やすことになってしまう。では、金種は、どのような額面金額が良いのだろうか?

（1.1）頭数

始めに、頭数という語を「ある整数の一の桁から連続する0を取り去った数」と定義する。例えば、300の頭数は3、81の頭数は81、1050の頭数は105、となる。ここで、これらの頭数の桁数は、順に、1、2、3となっている。

計算量は、頭数の桁数に大きく左右される。例を挙げると、「400+70」は、同程度の数値であっても、「388+75」に比べて計算が楽である。「1300-800」、或は「70*30」などの計算も、それぞれ「1308-761」、「74*26」よりも素早く暗算できる。割り算とその他の計算は、金額の計算に於いては滅多に使われないため、ここでは考えない。0を除き、頭数の桁数は1が最小である。これは、 1, 2, ... 9, 10, 20, ... 90, 100, 200, ... といった数である。そこで、計算容易化の観点から、金種の額面も、これらの数に設定するのが良い。

通貨の中には、金25（頭数が25の金種）というものが存在する。ロシアの25ルーブル硬貨、アメリカの25セント硬貨（クオーター）などがその実例である。もし、金25が金額設定の最小単位であれば、これらの金種は意味を持つ。しかし、実際はそうでないため、これらの額面金額は奇異であり、金額の計算を複雑にしているだけである。つまり、金25は、合理性を失っている。

（1.2）欠かせない金1

ところで、ここで仮にY732（732円という金額）を揃える場合を想定してみよう。このとき、恐らく君は、この金額を「700+30+2」と捉え、百の桁で7を、十の桁で3を、一の桁で2を、揃えようとするだろう。このように、ある金額を揃えるときには、大抵の人は桁毎にその金額を揃えるのである。実際には、あらゆる金額を揃える状況が起こりうる。そこで、どの桁（一、十、百、...）でも、1, 2, ... 9の金額を、その桁の金種のみを使って揃えられることが必要である。このためには、金1を各桁に配置すれば良い。これは、既に全ての通貨で実際に行われていることであり、又、これ以外の解決法は無いと思われる。

（2）桁あたりの金種

EU諸国では、通貨はユーロであるが、その金種は、「0.01（1セント）, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500」の15種類である。一方、日本の円では、金種は「1, 5, 10, 50, 100, 500, 1,000, 5,000, 10,000」の9種類である（殆ど出回っていない2,000円を除く）。ここで、この2つの通貨には、ある違いが見られる。即ち、ユーロは三金組（1桁につき3つの金種の組み合わせ）であるのに対し、円は二金組である。

三金組は、二金組に比べ、買い物や他の現金取引の際に必要となる硬貨や紙幣の数が少なくて済むという利点がある。又、人々は、より少ない硬貨と紙幣が入った財布を持ち歩くことができる。しかし同時に、三金組は、二金組に比べてより多くの金種があるために、財布の中で、或は商店の金銭登録器の中で、貨幣の選別がし辛くなるのである。

先に二金組について話を進め、その後で三金組に触れる。金1は必須なので、次にすべきことは、桁ごとに他の金N（N=2, 3, ... 9）の中から最適なものを突き止めることである。そして、これらの最適な金Nと金1を総合すると、ある通貨に於いて最善の金種構成が出来上がるのである。

因みに、現在の世界の通貨は、殆どが金5を設けており、金2を設けているものも見られる。5と2という数は、共に10の約数である。しかし、このことは貨幣を使用するときには全く意味を成さない。貨幣を使用するときは、硬貨や紙幣それ自体を数えるのであって5本の指を折って数えるのではない。又、金1をより小さい金種と両替するとき、1種類のみの金種と交換しなければならない、ということもない。この先入観のために、人間は今まで、この論文がやろうとしていることに気付かなかったのだが、君がこの論文を読み進めるためには、先ずこの先入観を捨て去ることが必要である。

（3）貨桁に於ける試験

金種構成の効率性を綿密に調査するため、硬貨と紙幣を別々に吟味する。ところで、この惑星上の全ての通貨は、硬貨又は紙幣の何れかの形態をしている。そして、私の知る限り、例外なく、硬貨は金額の低い桁に、紙幣は金額の高い桁に用いられている。この慣例には、然るべき理由があるようである。即ち、小さい物には低い価値を与え、大きい物には高い価値を与えているのである。又、安価な物は乱暴な扱いに備えて丈夫にし、逆に丁重な扱いが予期される高価な物には脆い材料を使用するのである。この点に関して、私は異論は無い。

硬貨の効率性に関しては、状況に応じて二つの指標がある。一つは、払人（貨幣を支払う人）が所持する「貨量」（硬貨の量（質量或は体積））であり、もう一つは、現金取引に於ける計算負荷を表す「算荷」である。貨量も算荷も、小さいほど良い。それは、貨量が小さければ、人々が持ち歩く財布がより軽くよりコンパクトになるからである。又、算荷が小さければ、支払いの際に現金の扱いがより短時間で済むようになるからである。

全ての現金取引に於ける支払いは、二つの型に分類される。払丈型（釣りが認められない現金取引）と、払釣型（釣りが認められる現金取引）である。尚、釣りが認められる取引に於いて、釣りなしで現金を支払う場合は、払釣型に含まれる。払丈型の比率は、払釣型の比率に比べてかなり小さいと予想される。何故なら、殆どの現金取引では釣りが認められており、そうしないと、自動販売機を含む小売商は、潜在的な顧客を逃してしまうかも知れないからである。

（3.1）試験A: 貨桁に於ける払丈型の貨量

貨量は、「持貨数」（払人が所持する硬貨の数）のみならず、硬貨の質量及び体積にも影響を受ける。硬貨の質量及び体積は、通貨によって、又金種によって異なるものの、どの硬貨も地球人が扱うのに丁度良い大きさをしているようである。この点で、貨量を小さくする目的で、或は硬貨の鋳造費用を削減する目的で、全ての硬貨を非常に小さく作ることは、誤った考えであると言える。理想的な硬貨の大きさがどの程度かという問題は、この論文のテーマではない。

ここでの論点は、硬貨の「N:1比率」（同じ桁にある金Nと金1の量の比）である。貨量を計算するに当たり、予めN:1比率を定めなければならない。私は、世界の幾つかの硬貨について、それらの質量と体積を調べた。その結果は、硬貨の測定にある。N:1比率は、1を下回る程小さいものから、5という高いものまで、かなり幅があるため、私は算術平均の代わりに幾何平均を取った。すると、質量のN:1比率の平均は、1.70となり、体積のN:1比率の平均は1.53となった。これら2つの幾何平均は、1.61である（表1-15）。そこで、貨量は、「持貨数N（N円玉の持貨数）の1.61倍と持貨数1の合計」と定義する。この1.61というN:1比率は、全ての貨桁（硬貨の桁）で使用する。硬貨の低い桁と高い桁とで、N:1比率を区別することは必要無さそうだからである。

払丈型の貨量を調査するために、円硬貨を用いた試験Aを準備する。ここで、試験Aは、1円桁のみを対象としている。さて、十分な数の1円玉とN円玉があるとしよう。Nは、2, 3, ... 9の何れかである。つまり、二金8組（8つの二金組）が競い合うのである。試験Aでは、先ず、釣りなしでY1, Y2, ... Y9を揃えるときの最小持貨数を数える。次に、持貨数Nの1.61倍と持貨数1を合計して貨量を計算する。このように敢えて2段階に計算するのは、実際に払人が頭の中で行う計算を模倣するためである。即ち、殆どの人は、N:1比率については頭に無く、持貨数に注意を払うであろう。この計算手順は、ここでは違いを生じないが、後に別の試験に於いて影響がある。

表2-1は、1,5組（金1と金5から成る二金組）の試験Aを示している。1,5組では、1円玉と5円玉が用いられる。例えば、Y7を揃えるときの貨量は、2+1.61=3.61となる。そして、Y1~Y9を揃える貨量の合計は、28.05となる。このようにして、他の組についても同様に貨量を調査した。その結果は、表2-2にある。

（3.2）試験B: 貨桁に於ける払丈型の算荷

続いて、二金8組の算荷について調べる。ここでは、硬貨の質量と体積は重要ではない。算荷は、主に動貨数（現金取引中に移動する硬貨の数）が関係する。この移動する硬貨には、払う硬貨と釣り硬貨の両方が含まれる。しかし、算荷には、他にも考慮すべき要素がある。それは、金額の計算しやすさである。そしてこれは、金1と金Nとで違いがある。100円玉を例に取ると、100円玉1個の金額はY100、100円玉2個はY200、3個ではY300、という具合に、金額の頭数は常に持貨数1の頭数と等しくなる。それとは反対に、金Nについては、金額の頭数が持貨数Nの頭数と等しくなることはない。これこそ、金1が金額を数えやすい理由なのである。

上記の点を踏まえ、算荷の計算では、頭数N（N=2~9）の硬貨を実際の数の1.5倍に数えることとする。金額の計算しやすさは、金Nの間でも差があるかも知れないが、それらの差は、金1と金Nの差に比べれば相当に小さいであろう。そこで、1.5という係数は、全ての金Nに一律に適用する。すると、算荷は、動貨数N（N円玉の動貨数）の1.5倍と動貨数1の合計となる。釣りなしでY1~Y9を揃えるときの最小算荷の合計を計算したのが試験Bである。試験Bの結果は、表2-3及び表2-4に示されている。

（3.3）試験C: 貨桁に於ける払釣型の貨量

払釣型のために、私はコンピュータの助けを借りて模擬取引の試験を実施した。試験Cは、二金8組がどれだけ平均貨量を少なくできるかを検査する。又、試験Dは、平均算荷の小ささを検査する。これらの試験では、実際の現金取引と同様に、揃える金額が1円桁のY1~Y9から無作為に選択される。ここで、現実には出現するY0は、1円桁に全く影響しないため、省略した。私は、模擬取引で使用する1~9の乱数100,000個を発生させ、連続100,000回の現金取引を行った。乱数の1~9への配分を表2-5に示す。

試験Cと試験Dに於いては、各取引での持貨数1と持貨数Nは、そのまま次の取引に持ち越される。コンピュータの中の払人は、幾つかの1円玉とN円玉に加え、十分なだけの10円玉を所持している。この10円玉は、本物の払人が携帯する財布の中にある10円以上の全ての金種を代表している。しかし、持貨数10は、貨量と算荷の計算には含められない。これは、10円桁の問題になるからである。

最小の貨量を調べる試験Cでは、払人は毎回、持貨数を最小にするよう努める。表2-6に、1,6組の模擬取引が進行する様子を例として示す。あるとき、払人は、6円玉0個と1円玉2個、それに沢山の10円玉を所持していたとする。最初に揃えるべき金額はY3で、払人は、10円玉を払い、釣りとして6円玉1個と1円玉1個を受け取る（これを「10-6-1」と表記する）。その結果、払人の手元には、6円玉1個と1円玉3個が残る。次に揃える金額はY8で、払人は、持貨数をより少なくするため、10-1-1ではなく6+1+1と支払う。すると、手元には6円玉0個と1円玉1個が残る。次に来たのはY5であるが、持貨数を最小にするため、10-1-1-1-1-1ではなく10+1-6が選択される。そして、払人の手元には6円玉1個と1円玉0個が残る。次はY4を揃えるが、ここで、6-1-1と10-6は持貨数が等しい。このような場合、払人は1円玉よりも6円玉（N円玉）を優先して減らす。

こうして、二金8組について模擬取引の試験が実施された。ここで、揃えるべき金額100,000個のY1~Y9の出現順、及び取引開始時に払人がN円玉0個と1円玉0個を所持していることは、何れの組も同じにした。尚、これらの条件は、他の模擬取引の試験に於いても同様である。試験Cでは、試験Aのときのように、貨量の計算に於いて持貨数Nは1.61倍される。表2-7に、全二金組の試験Cの結果を示す。

（3.4）試験D: 貨桁に於ける払釣型の算荷

試験Dは、払釣型の最小算荷を追求するが、これもコンピュータ・シミュレーションである。試験Dに於いて、払人は、毎回の取引で算荷が最小となる払い方を選択する。しかしながら、10円玉と釣りが存在するため、算荷は試験Bのときとは違いがある。試験Dを行う前に、計算負荷をより適切に反映させるため、新たな変数「倍桁」を定義する。倍桁は、金額が上の桁に影響するときは計算が複雑になる、という考えに基づいている。この具体例は、次段落に記載する。倍桁の導入によって、算荷は、動貨数Nの1.5倍と動貨数1、それに倍桁の合計となる。

1,8組の場合、コンピュータによる現金取引は、表2-8のようにに進行する。あるとき、払人は8円玉0個と1円玉1個、それに十分なだけの10円玉を所持していたとする。さて、最初に揃えるべき金額はY9で、払人は10-1と支払う。すると、払人の手元には8円玉0個と1円玉2個が残る。この取引では、支払金額（10円玉を含む）がY9を超えて10円桁に及ぶため、倍桁は1である。そして算荷は、1+1=2となる。次に揃える金額はY2で、払人は、最小の算荷を選択するため、10-8（算荷=2.5）ではなく1+1（算荷=2）と支払う。支払金額がY9以下のときの倍桁は0である。その結果、払人の手元には8円玉0個と1円玉0個が残る。次の金額はY4で、10+10-8-8という払い方が選択される。ここで、支払金額が10円桁に達するが、釣り金額（10円玉を除く）もY9を超える。このようなとき、倍桁は2となる。

表2-9は、全二金組の試験Dの結果である。ところが、試験Dの持貨数には問題がある。例えば、1,7組の試験Dでは、100,000回の取引後、払人が10,000個以上の1円玉を所持することになる。他の二金組も、時折、持貨数が数十に達する。表2-10を見よ。このような状況は、現実には起こりえない。

（3.5）試験E: 貨桁に於ける払釣型の修正算荷

従って、払人は、最小の算荷を選択し続けることはできず、別の払い方をしなければならない。私は、試験Dの支払い方法を見直し、試験Eを準備する。試験Eのシミュレーションでは、払人は通常、持貨数1と持貨数Nに応じて最小の算荷を選択する。しかし、持貨数1が5を超えたときは、払人は釣りの1円玉がなるべく少ない払い方に変更する。持貨数Nが5を超えたときも、同様に払い方を変更する。持貨数が溢れないようにする他の方法も考えられるが、算荷の上昇を最小限に抑えるために、私はこの方法を採用した。表2-11は、1,3組を例に、試験Eの一部を説明している。

試験Eの結果は、表2-12にある。各二金組の算荷は、試験Dの算荷に比べて幾分大きくなっているが（表2-9）、全ての持貨数は制御されている（表2-13）。

（3.6）高い貨桁に於ける試験

これまでの試験A~Eは1円桁で行われたが、この試験結果は、他の桁にも適用される。実際に、10円桁では、揃えるべき金額と使用される硬貨の額面金額が共に10倍になるため、1円桁の試験結果と同じ結果が得られる。100円桁についても同様である。

（3.7）貨桁に於ける評価

二金8組の試験結果を評価するため、私は「超‰」（超過千分率）を用いる。この数値は、貨量であれ算荷であれ、ある二金組の非効率性の程度を示す。超‰は値が小さいほど優れており、最善の超‰は0である。表2-2を参照せよ。

払丈型と払釣型の割合を考慮して、試験Aが5%、試験Bが5%,、試験Cが45%、試験Eが45%の割合で全試験の結果を統合する（表2-14）。最善の二金組は、断然、全ての試験で完璧な成績を残した1,4組であると判明した。仮に、試験A~Eが違った割合で統合されても、1,4組の1位は揺るがない。2位には1,6組が入り、1,7組と1,3組がそれに続いた。その一方、21世紀の人類が猶も選択している1,5組は、5位に終わり、その効率の悪さを露呈した。

（4）幣低桁に於ける試験

幣桁（紙幣の桁）に於いても、貨桁での試験と同様の試験を通して二金組の効率性について調査する。硬貨の試験での貨量は幣量（紙幣の量）と名前を変える。算荷は幣桁に於いても第2の指標である。幣桁での取引の型は、払丈型か払釣型であり、大部分が払釣型であることも貨桁と同様である。しかしながら、硬貨と紙幣の間には、幾つかの違いもある。

（4.1）減少する9個の度数

貨桁では、1~9の金額は実際の現金取引で等しい確率で出現すると想定し、この点に注意を払わずに試験A~Eを行った。実際に、Y1, Y2, ... Y9の度数は、殆ど等しいと考えられる。10円桁のY10~Y90も同じことであろう。100円桁は緩やかな下り傾斜があるかも知れないが、その影響は限定的であり、1,4組の優位を覆すには程遠いに違いない。因みに、0の度数は、二金8組を比較する際に意味を成さないが、他の数よりも若干高い可能性がある。何故なら、商品やサービスの値段は、しばしば切りの良い金額（頭数の桁数が小さい金額）に設定されるからである。

幣桁に於いては、1~9の度数は均等ではない。価格が高くなると、購買自体減少するが、加えて現金取引も減少する。その結果、小さい数の度数が高くなり、大きい数の度数が低くなる。そして、9個の度数は、「減9度」（減少する9個の度数）となる。

（4.2）補充される金種

幣桁は、減9度という点のみならず、人々が必要なときに銀行口座又は家の金庫から紙幣を補充するという点でも、貨桁と異なっている。補充される金種の桁によって、私は幣桁を「幣低桁」（紙幣の低い桁）と「幣高桁」（紙幣の高い桁）の2つに分類する。幣低桁は、紙幣が補充されない桁である。そして、幣高桁は、金Nが補充される桁である。

例えば、イギリスの人々は、20ポンド紙幣又は50ポンド紙幣を補充するだろう。この場合、10ポンド桁は幣高桁になる。もし、君がEU諸国に居住していて、20ユーロ又は50ユーロを補充し、100ユーロとそれより高額の紙幣を持ち歩かないのなら、10ユーロ桁は幣高桁になる。しかし、もし君が100ユーロを補充するのなら、10ユーロ桁は幣低桁になる。そして、仮に200ユーロ又は500ユーロを補充する場合は、10ユーロ桁が幣低桁、100ユーロ桁が幣高桁になる。このように、幣低桁と幣高桁は、現金使用の習慣の違いから、人によって変化することがある。

金1が補充される桁は、幣低桁にも幣高桁にもならない。もし、君が前段落の中で、100ユーロ紙幣を補充するとき、100ユーロ桁は何れの幣桁でもない。金1しか存在しない桁では、各二金組によって違いが生じないため、それらを比較する必要性がないのである。では、初めに幣低桁を研究する。

（4.3）対数正規分布に基づいた減9度

減9度の形は、対数正規分布であると予想される（図1）。これは、典型的に、収入と人口の関係を表すものとして説明される連続確率分布関数である。私は、幣低桁の減9度を設定するため、この関数を利用する。しかし、減9度の減少率は、現実に即したものとするために、どの程度にするのが良いのだろうか?

図1

対数正規分布

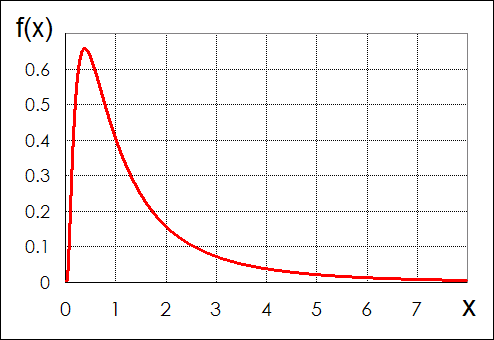
¤ f(x)=1/x/√(2πe^(log(x))²). μ=0. σ=1.
¤ 最頻値=1/e=0.368. 中央値=1. 平均値=√e=1.649.

高価な買い物でも現金で支払う人がいる。その一方、買い物の多くをクレジットカードや電子マネーで支払い、安い買い物のみに現金を使用する人もいる。従って、ある桁の減9度は、人によって様々である。このような減9度の多様性を反映させるため、対数正規分布に基づいた緩い減9度、中庸の減9度、急な減9度を用意する。表4-1、4-2、4-3を見よ。次に、これら3つの減9度の平均を取り、幣低桁で使用する減9度を設定する（表4-4、図2）。

図2

急、中庸、緩い、及び平均の減9度

ここで、対数正規分布に基づいた減9度の実用例を示す。例えば、現金によらない支払いが日常的であるアメリカ合衆国に、最頻値=$4、中央値=$10、平均値=$16という現金使用の習慣を持つ女性がいるかも知れない。この場合、緩い減9度が、彼女の現金取引の1ドル桁をうまく説明する。又一方で、ブラジルから遠く離れているにもかかわらず、未だに現金（real money）が幅を利かせている日本では、ある男性は大抵の買い物を現金で済ませるかも知れない。彼のデータは、最頻値=Y900、中央値=Y2,500、平均値=Y4,100となっている可能性がある。彼の現金使用の1,000円桁は、正に、急な減9度に符合する。

（4.4）試験A2: 幣低桁に於ける払丈型の幣量

幣量は、持幣数（払人が所持する紙幣の数）と、各紙幣の量に基づく。紙幣の量は、殆ど、紙幣の面積（長辺*短辺）によって決まる。紙幣の厚さ及び質量は、日常的な使用に関しては、紙幣の量にほんの僅かな影響しか与えない。そこで、私は、世界の紙幣について、その面積を調査した。紙幣の測定を見よ。ここで重要なことは、面積それ自体ではなく、N:1比率である。全てのN:1比率は、1若しくはそれよりもう少し大きい値に集中していたが、硬貨のN:1比率の場合と歩調を合わせるため、私は幾何平均を採用した。N:1比率の平均は、1.06となった（表3-15）。従って、幣量は、持幣数N（N円札の持幣数）の1.06倍と持幣数1の合計として定義される。

試験A2は、幣低桁のための試験Aである。試験A2に於いて用いられる金種は、架空の1円札とN円札である。例えば、1,3組の試験A2では、1円札と3円札を用いてY1~Y9を釣りなしで揃えるときの最小持幣数を数え、続いて幣量を求める。ここでの各幣量は、減9度が掛けられた上で合算され、合計幣量となる。表4-5を参照せよ。全ての二金組の合計幣量は、表4-6に示されている。

（4.5）試験B2: 幣低桁に於ける払丈型の算荷

次は、二金8組に試験B2を試す。試験Bでは、算荷計算の際、動貨数Nを実際の1.5倍に数えた。ここでも、動幣数N（現金取引中に移動するN円札の数）を1.5倍に数える。これは、金1の数えやすさという特質が、硬貨に限られたものではなく、紙幣にも適用されるものだからである。試験A2と同様に、各算荷は、減9度が掛けられた上で合算され、合計算荷となる（表4-7）。試験B2の結果は、表4-8で見ることができる。

（4.6）試験C2: 幣低桁に於ける払釣型の幣量

試験C2は、払釣型の幣量を調査するコンピュータ・シミュレーションである。しかしながら、ここの試験C2では、1~9の度数は減9度である。私は、減9度の確率で配分された乱数を用意し（表4-9）、試験Cのように100,000回の取引を実行した。試験結果は、表4-10にある。不思議なことに、最大持幣数と平均持幣数は、試験Cのそれらの持貨数とかなり近似している（表2-7）。

（4.7）試験D2: 幣低桁に於ける払釣型の算荷

表4-9の減9度は、払釣型の算荷を調べる試験D2に於いても用いられる。試験D2の結果は、表4-11に示されているが、持幣数（取り分け1,8組のもの）は、試験Dの場合のように膨張した（表2-10、4-12）。そこで、私は、持幣数の増大を防ぐため、試験Eの論理を備えた試験E2を行った。表4-13は、欠陥のある試験D2の代わりとなる試験E2の結果である。試験E2の持幣数は、合理的な水準に抑えられている（表4-14）。

（4.8）幣低桁に於ける二金組の評価

幣低桁に於ける試験結果は、表4-6（試験A2）、4-8（試験B2）、4-10（試験C2）、4-13（試験E2）にある。二金8組の総合成績は、貨桁に於いて行ったように、これらの超‰の値を統合することによって評価される（表2-14、4-15）。1,4組は、試験A2で1,3組に負けた以外は全て勝ち、頂点に立った。2位には、試験全体で高得点をマークした1,3組が来た。1,7組は試験A2とB2以外で健闘して3位になった。その一方、有名な1,5組は3桁得点という無様な成績を記録した。

（5）幣高桁に於ける試験

幣高桁に於いては、現金取引は払丈型か払釣型であり、二金8組は幣量と算荷について試験を受けなければならない。これらは、幣低桁と同様である。しかし、幣量を調べる模擬取引の試験Cで、一つ問題がある。それは、幣高桁では人々が手動で金Nを補充するため、幣量を測定するための新たな手法が必要となることである。算荷のための模擬取引に関しては、以前の試験と同様に行うことができる。

（5.1）減少する30個の度数

幣高桁は、金Nが補充される桁である。これは、人々が幣高桁よりも高い桁の金額の現金取引を行わない、ということを意味する訳ではない。稀であるとしても、それは起こりうるのである。しかし、幣高桁より高い桁には、実際に、或は少なくとも事実上、金種は存在しない。従って、Y1~Y9に限って考慮するのでは、十分ではないかも知れない。この点を踏まえ、私は、対数正規分布に基づいた減30度（減少する30個の度数）を準備した（表5-1）。

人々は、大抵、自分にとって最大の金種を補充するので、減30度の減少率は、減9度に比べて相対的に安定しているはずである。そこで、私は、唯1種類の減少率を用いて減30度を設定する。幣高桁は幣低桁よりも高いため、減30度の傾斜は、減9度の傾斜よりも急になる。

実際上、減30度が意味を成すことがある。ヨーロッパに、20ユーロ紙幣又は50ユーロ紙幣を補充する男性がいたとしよう。この例では、10ユーロ桁が幣高桁になる。もし、彼が日々の生活で、最頻値=€5、中央値=€13、平均値=€21という現金の使い方をしているならば、彼の幣高桁は、丁度、減30度に適合する。

（5.2）試験A3: 幣高桁に於ける払丈型の幣量

払丈型の幣量のため、試験A3（試験A2に減30度を適用したもの）を準備する。幣量は、1円札とN円札を用いて釣りなしでY1~Y30を揃えるときの最小持幣数から計算される。ここでは10円札が不在である点に注意を要する。表5-2は、1,4組の試験A3を示す。幣低桁の試験Aのように、持幣数4（持幣数N）は1.06倍に数えられる。1,2組から1,9組の試験A3の結果は、表5-3にある。

（5.3）試験B3: 幣高桁に於ける払丈型の算荷

次に来る試験は、幣高桁に於ける払丈型の算荷を研究する試験B3である。試験B2と同様、算荷は、動幣数Nの1.5倍と動幣数1の合計である。そして、Y1~Y30を揃えるときの各算荷は、減30度が掛けられた上で合算され、合計算荷となる（表5-4）。その他の二金組の試験結果は、表5-5に示されている通りである。

（5.4）試験C3: 幣高桁に於ける払釣型の幣量

試験C3は、幣高桁に於ける払釣型の幣量を調査するための模擬取引の試験である。ここでの揃える金額はY1~Y30であるが、これらは無作為に出現する。私は、減30度を模した1~30の乱数100,000個を用意した（表5-6）。そして、平均幣量を得るため、コンピュータに連続100,000回の現金取引を実行させた。試験C3では、払人は何枚かの1円札とN円札を所持している。10円札は存在しない。

模擬取引の最中、払人は、手元の金額が次回の取引金額を下回った場合、金Nを補充する。ここで重要なことは、補幣数（補充する紙幣の数）ではなく、補幣額（補充する紙幣の金額）である。では、払人は、一度に幾らを補充したら良いのだろうか?

現実の世界では、もし、人々が次回の現金取引に必要な最小限の金額しか所持していないとしたら、彼らはかなり頻繁に、財布に現金を補充しなければならなくなる。そのようなことは、ありそうもない。従って、人々は、補充する際、幾らかの金額を上乗せすることになろう。その一方で、もし、平均して10かそれを超える金額の金Nを補充する人々が多く存在するとしたら、1つ上の桁に金種が用意されていそうなものである。その結果、人々は、金Nの代わりに、その上の桁にある金1を補充することになろう。すると、幣高桁は幣低桁へと変化する。故に、幣高桁の平均補幣額は、10かそれよりも少ないと予想される。

（5.5）三つの試験C3

先ず、補幣額の多様性に対応するため、三つの試験C3を用意する。試験C3.2では、補幣数は、「次回取引の不足金額にY2を加えた金額」に達する、N円札の最小枚数である。2番目の試験C3.4では、追加金額がY4である。3番目の試験C3.6では、余裕分がY6である。

表5-7は、1,2組の試験C3.4を示している。模擬取引の中でどのように2円札が補充されるのかが、ここで説明されている。三つの試験結果は、表5-8、5-9、5-10で入手可能である。試験C3.2及び試験C3.4の平均補幣額は、殆どが10を下回っており、試験C3.6では、これが10前後である。この三つの試験は、実際の補幣額の多様性を良く反映しているようである。

次に、三つの試験C3の幣量を平均し、これを試験C3の幣量とする。この幣量は、幣高桁に於ける幣量の実際値を良く示しているだろう。二金8組の成績は、表5-11で計算されている。

（5.6）試験D3: 幣高桁に於ける払釣型の算荷

試験D3は、幣高桁に於けるもう一つの模擬取引の試験である。取引は、減30度の乱数を使って実施される（表5-6）。試験D3では、払人は何枚かの1円札とN円札を所持している。10円札は存在しない。これらの条件は、試験C3と同様である。表5-12は、1,5組を例に、模擬取引の進行を示している。試験結果は、表5-13にある。

（5.7）試験E3: 幣高桁に於ける払釣型の修正算荷

試験D3では、払人は毎回、最小の算荷を選択する。しかしながら、試験D及びD2に続き、ここにも欠陥が生じている。それは、先の試験の場合に比べるとそれほど深刻な問題ではないのだが、幾つかの二金組で、持幣数1が時折10を超えることである（表5-14）。そこで、私は試験D3を試験E3へと改良した。例えば、1,7組の模擬取引は、表5-15のように進行する。表5-16及び5-17に試験E3の結果を示す。全ての持幣数1は、適切に制御されている。

（5.8）幣高桁に於ける二金組の評価

幣高桁では、払丈型と払釣型の割合は、幣低桁や貨桁と変わりないだろう。従って、試験A3、B3、C3、E3を5:5:45:45の割合で混合し、幣高桁に於ける総合成績とする。表5-18を見よ。幣高桁では、次第に勢いを増していた1,4組を振り切り、1,3組が辛うじて1位でゴール・インした。その他の二金組は、先頭から大きく遅れた。1,5組は、額面に3個目の生卵を食らった。

（6）最善の二金組

私はこれまでのところ、貨桁、幣低桁、及び幣高桁に於ける二金組の効率性を調査してきた。結果を実用化するためには、幣低桁と幣高桁を一つに統合しなければならない。何故なら、仮に、ある通貨の幣桁に二種類の二金組があったとすると、人々が紙幣を取り扱うとき、より多くの間違いをしてしまうことが目に見えるからである。

（6.1）幣桁に於ける二金組の評価

幣桁に於ける二つの結果を統合するために、幣低桁と幣高桁の合成比率を設定しなければならない。しかし、この比率は、通貨によって異なるし、又、人によっても差異がある。そこで、私は、紙幣の測定にある紙幣のデータを利用して、幣低桁と幣高桁の比率の平均値を推測した。

私は、人々の半数が最大金種を補充し、残りの半数が2番目に大きい金種を補充する、と仮定した。そして、幣低桁と幣高桁の比率を推定するため、紙幣の金種数に応じて14の通貨を分類した（表5-19）。比率は、29対14となった。これを受けて、幣低桁と幣高桁の超‰の値をこの比率で合成し、幣桁の総合結果とする。表5-20を見よ。

1,4組は、1,3組と接戦の末に競り勝ち、幣桁で優勝者の称号を手にした。その他の3桁得点組は、どうでも良い。幣低桁と幣高桁の比率は、私の推測に基づいていたが、仮に、この比率が1:1程に低くても、4:1程に高くても、順位表の概観は殆ど変化しない。

（6.2）硬貨の高い桁に於ける減9度の可能性

二金組についての議論を終える前に、私が（4.1）段落で言及したことを確かめておく。それは、100円桁では、9個の度数が緩い下り傾斜になっているかも知れない、という点である。そこで、硬貨の高い桁に於いて度数が減少している場合に備え、試験A4及びC4（減9度による試験A及びC）を実施する。減9度を適用した試験B及びEについては、試験B2及びE2と同じ結果になることに注目すべきである。

表2-15は、1,4組の試験A4を説明している。二金8組の試験A4の結果は、表2-16にある。表2-17は試験C4の結果であるが、試験Cとの間に不思議な類似が見られる（表2-7）。これら新試験の結果は、表2-18上で合成され、減9度かも知れない貨桁に於ける二金組の成績を提供する。

表2-18にある全ての二金組の総合成績は、表2-14のものと概ね類似している。しかし、超‰は、以前の貨桁の試験にもっと近い数値になるはずである。何故なら、高い貨桁に於いて度数が減少しているとしても、それは高々緩い減9度であると予想されるからである。何れにせよ、1,4組は、貨桁に於いては無敵の強さを誇り、完璧な記録を維持した。

（6.3）二金組の結論

これまでの議論は、貨桁に於いても幣桁に於いても、1,4組が最善の二金組である、という結論を導いた。例えば、各桁の1,4組をまとめてみると、円の金種は、「1円、4円、10円、40円、100円、400円、1,000円、4,000円、10,000円」という構成になる。他の通貨についても、この例に倣う。

（7）1,3組の可能性

最善の二金組は1,4組であることが判明した。では、世界中の二金組の通貨は全て、現行の1,5組から1,4組に乗り換えるべきなのだろうか? 他に選択肢はないのだろうか? 幣桁に於ける1,3組の優れた効率性に着目し、私はその実用化の可能性について検討する。

（7.1）幣桁のみ1,3組

最初に、硬貨と紙幣で構成が異なる金種を設定することが、頭に思い浮かぶ。即ち、硬貨には1,4組を、紙幣には1,3組を充てるのである。円を例に取ると、一連の金種は、硬貨が「1円、4円、10円、40円、100円、400円」、紙幣が「1,000円、3,000円、10,000円」となる。金属の金と紙の金は、物質的に明確な違いがあるため、二つの金Nが並存していても、現金の取扱いの際に間違いが起きやすくなることはないだろう。従って、このような選択は十分可能であると思われる。

（7.2）貨桁に於けるN:1比率の見直し

貨桁の試験では、私はN:1比率を1.61に設定した。しかし、この比率は、硬貨の測定にある通り、本当に幅が広い。もし、この比率が1.61よりも小さかったら、又は大きかったらどうであろうか? 材料使用の観点から、大きい比率は効率性が悪い。その上、N:1比率を大きくすると、人々が財布の中で硬貨を識別しやすくなるが、そうするためには、他の方法もある。

例を挙げると、オーストラリアの50セント硬貨は、円形ではなく12角形をしている。又、英国には特異な7角形の50ペンス硬貨が存在する。同じく英国の1ポンド硬貨は、2ポンド硬貨に比べて、直径が小さいが厚い。そして、日本の5円玉は、50円玉もそうであるが、中央部に穴が開いている。これらの工夫によって、たとえN:1比率が凡そ1であっても、即ち硬貨の体積と質量が近似していても、硬貨の識別を容易にすることが可能なのである。

ところで、N:1比率が1未満、即ち相対的に金1が大きく金Nが小さい、というのはどうであろうか? 現実に、そのような奇妙な金種は存在している。オーストラリアの1ドル硬貨は2ドル硬貨よりも重い（表1-1）。日本の10円桁も同様である（表1-6）。しかしながら、大抵の人は、このような事例について、直観に反している、或は何かおかしいと感じることだろう。そして、これらの例外には合理的な理由が見当たらない。そこで、私はN:1比率が1より小さい場合を検討しないこととする。

（7.3）貨桁に於ける試験A5及び試験C5

私は、金Nの量と金1の量が等しいと仮定して、試験A5及びC5を試す。N:1比率は1.61ではなく丁度1であり、貨量は単純に持貨数Nと持貨数1の和となる。これらの試験では、持貨数Nと持貨数1は、試験A及びCと同じである（表2-2、2-7）。従って、貨量は簡単に計算することができる（表2-19、2-20）。

（7.4）貨桁に於ける再評価

私は、貨桁に於ける二金8組を再評価するため、結果をまとめた。試験A及びCは、それぞれ試験A5及びC5に置き換えられる一方、試験B及びEはそのままである。総合結果は、表2-21に示されている通りである。1,4組が再び完全勝利を収めた。1,3組は、新試験でトップになり、勝者に比肩する一歩手前まで得点を伸ばした。

1,3組がその効率性の高さを証明した新たな試験結果を受けて、私は、第2位の二金組を全ての桁に於いて導入することに幾らかの根拠があることを認めざるを得ない。1,4組が最善の二金組であることは明らかであるが、1,3組も、全ての貨桁に於いてN:1比率がほぼ1であるという条件の下、もう一つの選択肢になり得る。円を用いて1,3組を例示すると、「1円、3円、10円、30円、100円、300円、1,000円、3,000円、10,000円」となる。

（8）三金組の一端

現在、21世紀の初期時点で、この惑星上の通貨は、事実上、二金組の1,5組か、或は三金組の1,2,5組か、の何れかである。しかしながら、二金組について行った試験から、1,5組は、頂上の1,4組に比べて遥かに効率が悪いことが判明した。それでは、1,2,5組はどうだろうか? 三金組の能力を探るため、手始めに試験A及びBを試してみる。三金組部門には、28の参加者がいる。これを三金28組と呼ぶ。

（8.1）三金組の貨桁に於ける払丈型の貨量

三金組の貨桁に於ける試験Aは、試験A6である。試験を開始する前に、私はN₁:1比率とN₂:1比率を定めなければならない。ここで、N₂はN₁よりも大きい。表1-15は、地球上にある三金組の硬貨のN₁:1比率とN₂:1比率を示している。幾何平均を計算した結果、N₁:1比率は1.45に、N₂:1比率は1.60に設定された。すると、貨量は、持貨数N₂の1.60倍、持貨数N₁の1.45倍、及び持貨数1、の合計となる。

表6-1は、1,3,4組の試験A6の結果を示す。それ以外の27の三金組の結果は、表6-2にある。金メダルを手にしたのは、1,4,6組であった。そして、敗者のうち7組は、超‰が50以内に入った。著名な1,2,5組は、17位でもがき苦しんでいた。

（8.2）三金組の貨桁に於ける払丈型の算荷

試験B6は、払丈型の算荷を調査する。例えば、1,4,5組の試験B6は、表6-3に示されている。ここで、算荷計算の際、動貨数4と動貨数5は、共に1.5倍される。三金28組の合計算荷は、表6-4で見ることができる。頂点には5組の競技者が並んだ。別の5組は、超‰=24で同点となり、第二集団を形成した。一方、1,2,5組は、又もや3桁得点をマークし、その非効率性を露呈した。

（8.3）三金組の幣低桁に於ける払丈型の幣量

次は、幣低桁に移り、払丈型の幣量のための試験A7を準備する。紙幣のN₁:1比率とN₂:1比率も又、実在する三金組の通貨の測定結果に基づいて決定される。表3-15の計算によると、平均のN₁:1比率は1.05となり、N₂:1比率は1.12となった。これを受けて、幣量は、持幣数N₂の1.12倍、持幣数N₁の1.05倍、そして持幣数1、の合計となる。

幣低桁に於いては、二金組であろうと三金組であろうと、1~9の度数は減9度である。よって、表4-4の減9度は、試験A7でも使用される。例えば、1,3,6組の幣量計算は、表6-5で詳しく説明されている。全三金組の幣量の成績を示す表6-6によると、1,3,4組が単独で勝利した。数十億人の落胆していた1,2,5組の利用者にとっては驚くべきことであるが、それは超‰が35で2位に入った。

（8.4）三金組の幣低桁に於ける払丈型の算荷

三金組にとって4番目の試験は、払丈型の算荷を研究する試験B7である。試験B6と同様に、動幣数N₁と動幣数N₂は1.5倍される。そして、算荷計算に於いて減9度が適用される点は、試験A7と同様である。表6-7は、1,2,5組の試験B7を示している。全三金28組の合計算荷は、表6-8にある。1,3,4組がどうにか単独のリードを保ち、競争に勝った。1,3,5組と1,3,6組は先頭の直後に付けた。1,2,5組は遅れを取り、相応の中流階級へと戻った。

（8.5）三金組の有力候補

ここで、私は立ち止まって三金組の4つの試験結果を振り返る。これまで行った試験は、払丈型のみであるが（表6-9）、この結果から、最善の三金組を推量することができる。貨桁に於いては、1,4,6組が試験A6及びB6で完全な記録を残した。すると、これが最有力候補である。1,3,6組、1,4,5組などのライバルは、払釣型の試験での逆転が可能な位置に付けている。他方、幣低桁に於いては、1,3,4組が、他の組に対して優位を保っており、最善の三金組のようである。

（9）二金組か三金組か

最善の三金組は、貨桁と幣桁で異なるようである。しかしながら、残りの試験の結果、貨桁に於いては1,4,6組が、又幣桁に於いては1,3,4組が、それぞれ総合優勝したと仮定しよう。そのとき、二金組の1,4組と、最善の三金組ペアは、どちらがより効率的なのだろうか? この質問に答えるのは、一見すると難しそうである。しかし、ここに一つの手掛かりがある。それは、現行の金種構成である1,5組と1,2,5組は、世界中で競い合っていることから、これらの効率性の水準はかなり近いと予想されることである。この仮定に基づくと、勝敗は、各最善の組がどれだけ現行の組を上回るかによって決せられる。

表2-14によると、貨桁の試験に於ける1,4組と1,5組の超‰の差は、79である。そして、幣桁の試験に於けるその差は、103である（表5-20）。それに対して、1,2,5組は、超‰のトップとの差は、129（表6-2）、119（表6-4）、35（表6-6）、そして90（表6-8）である。ここで得られる数値から判断すると、二金組と三金組は、改善の程度が同じくらいである。従って、どちらが優れているかは、判断しがたい。

（9.1）決定的な要素

三金組を更に調査することで、本当の全体像が判明するだろう。しかしながら、そのような大変な労力を要すると見込まれる作業をせずとも、私は別の論理によって結論を確信しているのである。（2）段落で述べたように、二金組は、硬貨と紙幣の数に問題がある。他方、三金組は、金種の多様さが悩みの種である。ここで、1,4組は、二金組の弱点を最小限に抑えることに成功した。しかし、最善の三金組は、元来の長所をより強固にしたものの、固有の欠陥については全く改善がない。三金組が二金組と競うためにすべきことは、その障害を取り除くこと、即ち、金種を削減し、二金組へと転向することである。故に、全ての組は、二金組であろうと三金組であろうと、結局、1,4組に辿り着くのである。

（9.2）三金組への拘り

もし、ある三金組の貨幣制度が、何らかの理由で二金組に生まれ変わることをためらう場合は、それは三金組に固執することもできる。しかしながら、私は、そのような三金組信者のために、これ以上、最善の三金組を捜し求めるつもりはない。私は、彼らに対しては、唯、無駄の多い慣習に見切りをつけ、1,3,4組でも、1,4,6組でも、或は和音を奏でているように聴こえる何かの新たな組でも、試してみることを勧める。1,4組が間違いなく本道であるが、現状に比べれば、より良い三金組の道も何本か存在する。

（9.3）前提条件

この論文中の議論は、21世紀時点の地球人にとって有意義である。しかしながら、ここには二つの前提条件が存在する。第一の前提は、十進数表記である。第二は、金種が硬貨と紙幣という2形態で構成されていることである。これらの土台は、当面の間、安定していると思われる。万が一、何らかの変化が生じた場合は、1,4組を追い越す三金組が出現することになろう。

例えば、人間社会に十六進法が導入されたとしよう。すると、二金組は、ある桁の1から15までの金額に対応するため、もう一つの金種が欲しくなるだろう。それに対して、硬貨、紙幣以外の第三の形態の金が地上に現れた場合、硬貨と紙幣は、金種の一部を新しい金に譲らなければならない。その結果、人々は、三金組の多様な金種を扱うことに、従来よりも不便を感じなくなることだろう。将来、そのような大変動が発生した場合、私の研究は再検討を要することになろう。

（10）結論

最後に、私の研究が到達した幾つかの重要な結論を、ここに列挙する。

（1）1,4組こそが、貨桁に於いても幣桁に於いても、最善の金種構成である。

（2）幣桁に於いては、1,3組も、代替手段になり得る。

（3）1,3組は、全ての貨桁のN:1比率がほぼ1であるという条件の下、幣桁のみならず貨桁に於いても、選択肢になり得る。

（4）1,5組と1,2,5組は、何れも、この惑星から既に絶滅していたとしても不思議ではないほどに、効率が悪い。

略語

1,5組: 金1と金5の組み合わせ
N:1比率: 同じ桁にある金Nと金1の量の比
Y732: 732円という金額
頭数: ある整数の一の桁から連続する0を取り去った数
貨桁: 硬貨の桁
貨量: 硬貨の量; 持貨数とN:1比率に基づく。
金25: 頭数が25の金種
減30度: 減少する30個の度数; 幣高桁の試験で使用される。
減9度: 減少する9個の度数; 幣低桁の試験で使用される。
三金組: 1桁につき3つの金種の組み合わせ
三金28組: 28の三金組
算荷: 現金取引に於ける計算量
超‰: 超過千分率; 二金組及び三金組の非効率性を表す指標; この値が小さい程優れており、最善の超‰は0である。
動貨数: 現金取引中に移動する硬貨の数
動貨数N: N円玉の動貨数
動幣数N: 現金取引中に移動するN円札の数
二金組: 1桁につき2つの金種の組み合わせ
二金8組: 8つの二金組
倍桁: 2倍の桁; 算荷を調べる模擬取引の試験で用いられる変数; 0, 1, 2の何れかの値を取る。
払丈型: 釣りが認められていない現金取引
払釣型: 釣りが認められている現金取引
払人: 貨幣を支払う人
幣桁: 紙幣の桁
幣高桁: 紙幣の高い桁; この桁では金Nが補充される。
幣低桁: 紙幣の低い桁; この桁では紙幣が補充されない。
幣量: 紙幣の量; 持幣数とN:1比率に基づく。
補幣額: 補充される紙幣の金額
補幣数: 補充される紙幣の数
持貨数: 払人が所持する硬貨の数
持貨数N: N円玉の持貨数
持幣数: 払人が所持する紙幣の数
持幣数N: N円札の持幣数

1¤4

ある通貨に於ける効率的な金種構成
表1: 硬貨の測定
表2: 貨桁に於ける試験
表3: 紙幣の測定
表4: 幣低桁に於ける試験
表5: 幣高桁に於ける試験
表6: 三金組の試験