公認会計士短答式試験の合格倍率
島崎 崇
公認会計士短答式試験は、1995年から毎年実施されている。それ以降2013年までの短答式試験について、合格倍率を分析した。合格倍率は、試験の合格水準を反映する指標であるから、合格倍率の推移を見ることで、試験の合格水準の変化を知ることができる。尚、分析に用いた受験者数、合格者数等のデータは、公認会計士・監査審査会ホームページにある情報に基づいている。
短答式試験の合格倍率の推移
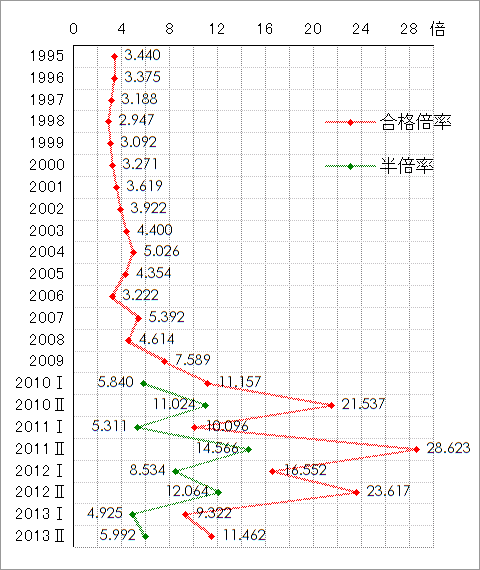
半倍率は、2010年以降に短答式試験が年2回化されたことを受け、合格倍率を約半分にしたものである(後述の非度外視法参照)。
短答式試験の合格倍率は、2008年までは比較的安定しており、若干の増加傾向が見られるが、2009年以降は狂ったように上昇している。2010年以降の半倍率でさえ、2008年以前の合格倍率とは異質な高い値を記録している。
公認会計士試験の目的は、公認会計士になろうとする者に必要な学識及びその応用能力を有するかどうかを判定することである(公認会計士法第5条)。2009年以降も、公認会計士になろうとする者に必要な学識及びその応用能力は変化していないことから、合格水準も変わっていない。その結果として、合格倍率も安定して推移するはずである。従って、合格倍率が急上昇した2009年以降の短答式試験は、公認会計士法第5条に反する違法試験である。
(参考)論文式試験の合格倍率の推移
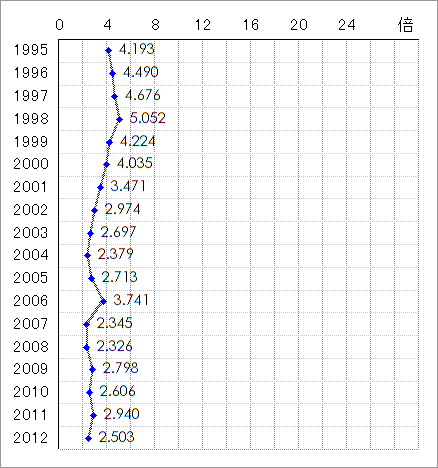
上図から、論文式試験の合格倍率は、緩やかに減少しつつ安定して推移していることが分かる。短答式試験の合格倍率が急上昇した2009年以降も、何事も無いかのように、低い値で極めて安定している。論文式試験については、短答式試験とは裏腹に、公認会計士法第5条を遵守して適正に運営されているのである。
短答式試験の合格倍率とZ値
短答式試験の合格倍率は、下表の通りである。Z値は、1995~2008年の合格倍率を基準にして、2009年以降の合格倍率の異常さを測定したものである。
| 年 | 願書 提出者 | 論文 受験者 | 合格 倍率 | Z値 |
|---|---|---|---|---|
| 1995 1996 1997 1998 1999 2000 2001 2002 2003 |
10,414 10,183 10,033 10,006 10,265 11,058 12,073 13,389 14,978 |
3,027 3,017 3,147 3,395 3,320 3,381 3,336 3,414 3,404 |
3.440 3.375 3.188 2.947 3.092 3.271 3.619 3.922 4.400 |
-0.522 -0.605 -0.845 -1.154 -0.968 -0.739 -0.293 0.095 0.709 |
| 年 | 受験 者数 | 合格 者数 | 合格 倍率 | Z値 |
|---|---|---|---|---|
| 2004 2005 2006 2007 2008 2009 2010.1 2010.2 2011.1 2011.2 2012.1 2012.2 2013.1 2013.2 |
16,269 15,284 16,210 14,608 16,217 17,371 17,583 17,660 17,244 14,970 13,573 10,722 9,984 7,966 |
3,237 3,510 5,031 2,709 3,515 2,289 1,576 820 1,708 523 820 454 1,071 695 |
5.026 4.354 3.222 5.392 4.614 7.589 11.157 21.537 10.096 28.623 16.552 23.617 9.322 11.462 |
1.511 0.650 -0.802 1.981 0.982 4.796 9.370 22.675 8.010 31.759 16.286 25.342 7.018 9.761 |
受験者数には、欠席者(願書を提出したが受験しなかった者)が含まれている。
1995~2003年は、短答式試験の受験者数、合格者数のデータが得られなかった。このため、公表されている願書提出者、論文式試験受験者のデータを用いている。願書提出者、及び論文式試験受験者の中に含まれている司法試験合格者等の短答式試験の免除者は数十人程度で、合格倍率への影響は極めて小さい。
2007年以降は、企業法のみの受験者が含まれている。この受験者は一般の受験者(3科目以上の受験者)に比べて合格倍率が著しく低いが、一部の年を除いて人数が不明であるため、これを含めたまま、合格倍率を算出した。一般受験者の合格倍率は、これよりも幾らか高くなる。
合格倍率は、合格率の逆数であり、受験者数を合格者数で除して求めることができる。例えば、2004年の合格倍率は、16269/3237=5.026 と計算される。
1995年から2008年までは、合格倍率は比較的安定しており、概ね、3~5前後(合格率は20%~30%前後)である。この期間の合格倍率は、平均値が3.847(合格率の平均値は25.99%)、標準偏差が0.780であった。
1995~2009年の合格倍率の標準偏差を求めると、1.224と跳ね上がる。このことからも、2009年以降の合格倍率は異常であり、1995年~2008年の合格倍率を基準とすることに合理性が認められる。
Z値は、標準正規母集団に於ける位置を表している。この標準正規母集団は、上記合格倍率の平均値3.847、及び標準偏差0.780を持つ母集団を正規化したものである。例えば、1995年のZ値は、(3.440-3.847)/0.780=-0.522 と計算される。
非度外視法
短答式試験が年2回行われるようになった2010年以降については、試験運営上、合格倍率を従来通りに保つ方法と、合格倍率を従来の約2倍に引き上げる方法とがある。前者は、試験が年2回になっても、試験科目、試験時間、受験手数料等が、従前と全く変わらないことを考慮し、又、試験の年2回化の意義を尊重した方法である。上表では、2010年以降についても、前者の方法に基づいて合格倍率及びそのZ値を算出ている。
その一方で、合格倍率を約2倍にする後者の方法は、受験者が合格するまでの学習期間を従来と同程度にすることで、合格者の水準を一定に保つことを想定した方法である。この場合、合格するまでの受験回数の期待値が増加するため、受験者は不利益を被る。又、一定数の合格者を決定するために、わざわざ2倍のコストを掛けるため、試験の年2回化の意義を完全に否定することになる。しかし、この方法によると、合格倍率の上昇をより慎重に判断することができる。
ここで、公認会計士法第5条によると、公認会計士試験は、公認会計士になろうとする者に必要な学識及びその応用能力を有するかどうかを判定することをその目的としている。そのため、公認会計士法第5条が遵守される結果、短答式試験合格者の水準、即ち合格倍率は、毎回の試験でほぼ一定に保たれることとなる。試験運営上最も重要なこの要素を考慮するか否かにより、後者を非度外視法、前者を度外視法と呼ぶ。非度外視法の場合、合格倍率は、次のように半倍率に変換される。
Y=y2/(2y-1)y: 実際の合格倍率
Y: 半倍率
合格倍率がyの試験を2回受験したとき、少なくとも1回合格する倍率がYである。
半倍率とZ値
非度外視法によって、2010年以降の半倍率とZ値を計算し直すと、次のようになる。
| 年 | 合格倍率 | 半倍率 | Z値 |
|---|---|---|---|
| 2010.1 2010.2 2011.1 2011.2 2012.1 2012.2 2013.1 2013.2 |
11.157 21.537 10.096 28.623 16.552 23.617 9.322 11.462 |
5.840 11.024 5.311 14.566 8.534 12.064 4.925 5.992 |
2.554 9.200 1.876 13.740 6.008 10.532 1.382 2.750 |
合格倍率の適正範囲
次に、1995年から2008年までの合格倍率を基準にして、合格倍率の適正範囲を検討する。ここでの論点は、2009年以降の合格倍率の異常な高さにあるので、適正範囲の下限は考えない。例えば、有意水準1%の場合、P(Z>2.326)=0.01であるから、合格倍率のZ値が2.326を下回ると、その合格倍率は適正範囲にあると判断される。このときの合格倍率の上限は、3.847+0.780*2.326=5.662となる。尚、合格率の適正範囲は、1/5.662=17.66%超となる。
非度外視法の場合は、半倍率の適正範囲が5.662未満となる。これに対応する合格倍率は、10.800未満である。又、合格率の適正範囲は、1/10.800=9.26%超となる。
短答式試験に対する意見表明
最後に、2009年以降の公認会計士短答式試験が適正に実施されたかどうかについて、合格倍率を分析した結果に基づいて、私の意見を表明する。
度外視法の場合、2009年以降は、どの試験に於いても、合格倍率が適正範囲の上限5.662を上回っている。よって、2009年以降の全ての短答式試験は、適正に実施されていないものと認める。この期間のZ値は、2009年のときに最小値4.796を記録している。従って、P(Z>4.796)=0.000000809より、仮に有意水準が百万分の一であっても、全ての試験が不適正であることに変わりはない。
一方、2010年以降の短答式試験について、非度外視法によって慎重に判断した場合の意見は、次の通りである。この場合、2013年までの8回の試験のうち、合格倍率が10.800を下回っている2011年第1回と2013年第1回の試験については、適正意見を表明することができそうである。しかしながら、会計専門職大学院を修了した3科目免除者を除外した場合、一般受験者の合格倍率が上昇することを忘れてはならない。
2011年第1回の試験については、別口受験者の割合が不明であるため、一般受験者の合格倍率が適正範囲を超えている可能性を否定し切れず、私は意見表明のための合理的な基礎を得ることができなかった。よって、私は、2011年第1回短答式試験が適正に実施されたかどうかについての意見を表明しない。
2013年第1回及の試験については、一般受験者の合格倍率にあるように、新たに公開された得点階層分布表から、裏口受験者の存在を考慮しても、一般受験者の合格倍率が10.800未満であるという心証を得ることができた。しかしながら、非度外視法の採用は、短答式試験の年2回化の完全否定を前提としていることを忘れてはならない。
2010年以降の受験者は、短答式試験の年2回化によって、受験手数料の倍増を始め、様々な負担の増加を強いられた。公認会計士・監査審査会は、これらの受験者に対して、受験手数料の半額返還等、適切な補償をしなければならない。しかし、同審査会は、未だ何の補償もしていないことから、試験の年2回化を肯定している状況にある。従って、現時点では非度外視法採用の前提に関する重要な不確実性が認められる。よって、私は、2013年第1回短答式試験については、上記事項の受験者に与える影響を除き、適正に実施されたものと認める。
残りの6回の短答式試験は、合格倍率が10.800を超えているため、これらの試験に対しては、不適正意見を表明する。更に、このうち2010年第2回、2011年第2回、2012年第1回及び第2回の試験に至っては、何れも半倍率のZ値が6を上回っている。P(Z>6)=0.000000000987であるから、仮に有意水準が十億分の一であっても、この4回の短答式試験は、不適正意見を免れることができない。
以上から、2009年以降の公認会計士短答式試験に対する意見をまとめると、下表のようになる。
| 年 | 度外視法 | 非度外視法 |
|---|---|---|
| 2009 | 不適正意見 | - |
| 2010.1 | 不適正意見 | 不適正意見 |
| 2010.2 | 不適正意見 | 不適正意見 |
| 2011.1 | 不適正意見 | 表明しない |
| 2011.2 | 不適正意見 | 不適正意見 |
| 2012.1 | 不適正意見 | 不適正意見 |
| 2012.2 | 不適正意見 | 不適正意見 |
| 2013.1 | 不適正意見 | 限定付適正意見 |
| 2013.2 | 不適正意見 | 不適正意見 |
公認会計士試験の合格率
一般受験者の合格倍率