Construction problem 2
With compasses and a straightedge, first draw a line segment, and then construct a point that divides the line segment internally in the ratio 1:2.
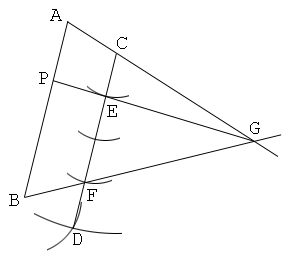
Solution 1
Constructing, a line segment that is parallel to the initial line, and a point that divides the line segment externally 2:3
1. Draw a line segment AB.
2. Put a point C. And put a point D so that a quadrilateral ABDC forms a parallelogram.
3. Draw a line CD, and put points E and F on this so that CE:EF=1:2 and EF<CF.
4. Draw a line AC and a line BF, and let G be the intersection of them.
5. Draw a line EG, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
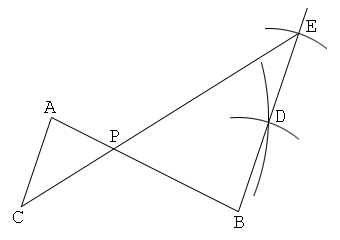
Solution 2
Constructing a pair of parallel lines each of which passes through either end of the initial line segment
1. Draw a line segment AB.
2. Put a point C. And put a point D so that a quadrilateral ACBD forms a parallelogram.
3. Draw a line BD, and put a point E on this so that BD=DE.
4. Draw a line CE, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
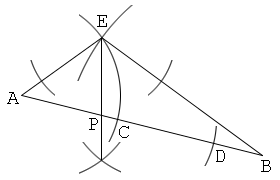
Solution 3
Constructing a triangle whose one side is the initial line segment, and the other sides are 1:2 in length
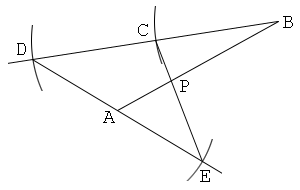
1. Draw a line segment AB.
2. Put points C and D, for example on the line AB, so that AC:AD=1:2.
3. Put a point E so that AE=AC and BE=AD. And draw a line EA and a line EB.
4. Draw a bisector of the angle AEB, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
Solution 4
Utilizing an isosceles triangle whose sides are 2:3:3 in length (1) (An isosceles triangle of 1:3:3 can be utilized instead.)
1. Draw a line segment AB.
2. Put points C and D on the line AB so that BC:BD=2:3.
3. Put a point E so that CE=BE=BD.
4. Draw a line BE. And put a point F on this so that BF=BA and AF//DE.
5. Put a point P on the line AB so that FP=FB. Then the point P divides the line segment AB internally in the ratio 1:2.
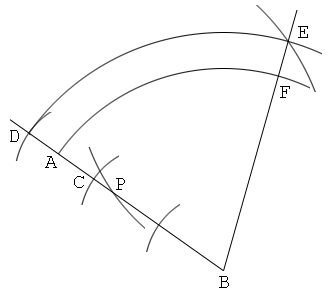
Solution 5
Utilizing an isosceles triangle whose sides are 2:3:3 in length (2) (An isosceles triangle of 1:3:3 can be utilized instead.)
1. Draw a line segment AB.
2. Put points C and D on the line AB so that AC:AD=2:3.
3. Put a point E so that AE=AD and DE=AC.
4. Draw a line AE. And put a point F on this so that AF=AB and BF//DE.
5. Put a point P on the line segment AB so that BP=BF. Then the point P divides the line segment AB internally in the ratio 1:2.
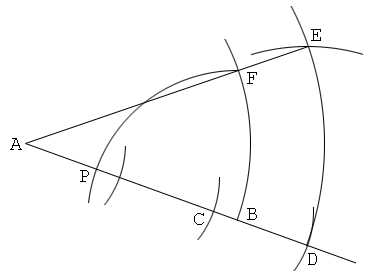
Solution 6
Determining points that are on the circumference of a circle whose center is a point to be constructed
1. Draw a line segment AB.
2. Construct a center point of AB, and let C be this.
3. Put points D and E, for example on the line AB, so that CE:DE=1:2.
4. Put a point F so that CF=CE and BF=DE.
5. Draw a perpendicular bisector of AF, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
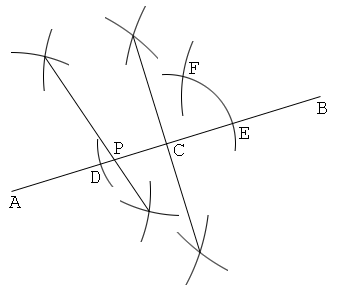
Solution 7
Constructing an equilateral triangle and its centroid, with its one side the initial line segment
1. Draw a line segment AB.
2. Put a point C so that AC=BC.
3. Construct a centroid of the equilateral triangle ABC, and let D be this.
4. Draw a perpendicular bisector of AD, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
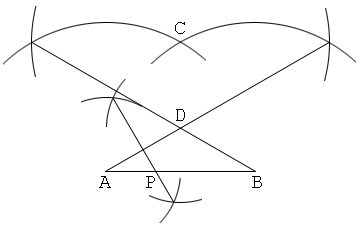
Solution 8
Utilizing that the centroid of a triangle cuts a line segment between one vertex of the triangle and the midpoint of the opposite side in the ratio 2:1
1. Draw a line segment AB.
2. Draw a line from B, and put points C and D on this so that BC=CD.
3. Draw a line DA, and put a point E on this so that DA=AE.
4. Draw a line EC, and let P be the intersection of this and AB. Then the point P divides the line segment AB internally in the ratio 1:2.
Mathematical Problems