Construction problem 3
With compasses and a straightedge, first draw two line segments, and then, letting 'a' and 'b' be the lengths of them, draw a line segment whose length is √(ab).
Solution 1
Utilizing (a+b)2-(a-b)2=4ab
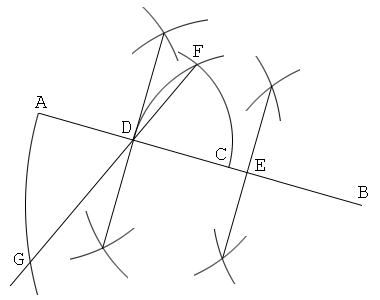
1. Draw a line segment AB, and put a point C on this. Let AB=a and BC=b.
2. Put a point D on an extended line AB so that BD=BC.
3. Draw a line from C that is perpendicular to AB, and put a point E on this so that AE=AD.
4. Construct a center point of CE, and let F be this. Then CF=√(ab).

Solution 2
Utilizing (a-b/2)2-(b/2)2=a2-ab, and a2-(a2-ab)=ab
1. Draw a line segment AB, and put a point C on this. Let AB=a and AC=b.
2. Construct a center point of AC, and let D be this. In addition, construct a center point of BD, and let E be this.
3. Put a point F so that DF=DC and EF=ED.
4. Draw a line DF, and put a point G on this so that BG=BA. Then FG=√(ab).
Solution 3
Utilizing (a-b)2+b2-2(a-b)b*cos120°=a2+b2-ab, and (a2+b2-ab)-(a-b)2=ab
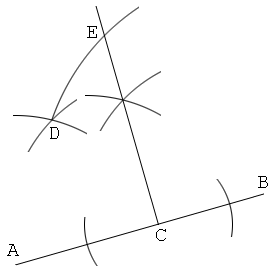
1. Draw a line segment AB, and put a point C on this. Let AB=a and AC=b.
2. Put a point D so that AD=CD=AC.
3. Draw a line from C that is perpendicular to AB. And put a point E on this so that BE=BD. Then CE=√(ab).
Solution 4
Utilizing a right triangle that is divided into two similar right triangles
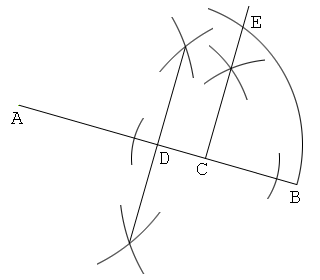
1. Draw a line segment AB, and put a point C on this. Let AC=a and BC=b.
2. Construct a center point of AB, and let D be this.
3. Draw a line from C that is perpendicular to AB. And put a point E on this so that DE=DB. Then CE=√(ab).
Solution 5
Utilizing, a line that intersects a circle at two points, and another line that touches the circle
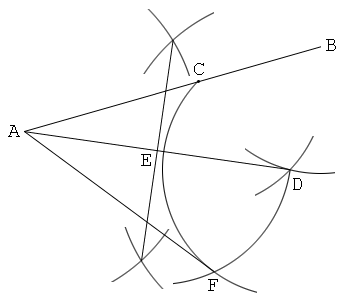
1. Draw a line segment AB, and put a point C on this. Let AB=a and AC=b.
2. Put a point D so that BD=CD.
3. Construct a center point of AD, and let E be this.
4. Put a point F so that DF=DC and EF=ED. And draw a line AF. Then AF=√(ab).
Mathematical Problems