Construction problem 4
With compasses and a straightedge, first draw a circular sector with its central angle less than 180°, and then construct an inscribed circle of the circular sector.
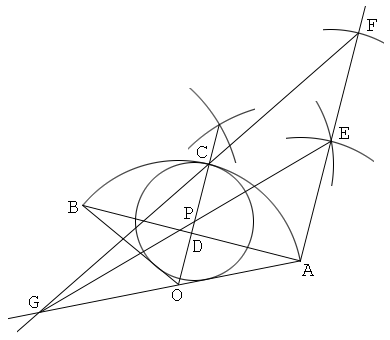
Solution 1
Constructing, a line segment that is parallel to the bisector of the central angle, and a point that divides the line segment internally in the ratio "the radius" to "half the chord" (cf. Solution 1 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E so that a quadrilateral OAEC forms a rhombus.
5. Draw a line AE, and put a point F on this so that EF=AD and AE<AF.
6. Draw a line CF, and let G the intersection of this and an extended line OA.
7. Draw a line EG, and let P the intersection of this and OC.
8. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
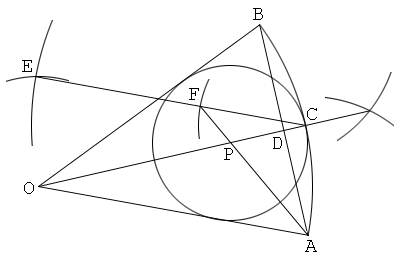
Solution 2
Constructing, a line that passes through the center of the circular sector, and another line that is parallel to the line and that passes through the midpoint of the arc (cf. Solution 2 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E so that a quadrilateral OACE forms a parallelogram.
5. Draw a line segment CE, and put a point F on this so that CF=AD.
6. Draw a line AF, and let P the intersection of this and OC.
7. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
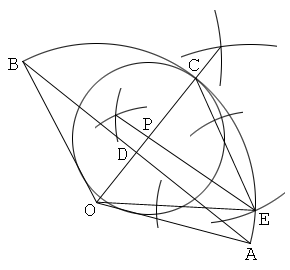
Solution 3
Constructing a triangle whose one side is the line segment between the center of the circular sector and the midpoint of the arc, and the other two sides are "the radius" to "half the chord" in length (cf. Solution 3 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E on the arc AC so that CE=AD. And draw a line EO and a line EC.
5. Draw a bisector of an angle OEC, and let P the intersection of this and OC.
6. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
Solution 4
Utilizing an isosceles triangle whose sides are x:y:y in length (1) (x="the radius of the circular sector" and y="the radius plus half the chord") (cf. Solution 4 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E on the line OC so that CE=AD and OC<OE.
5. Put a point F so that CF=OF=OE.
6. Draw a line segment OF. And put a point G on this so that OG=OC.
7. Put a point P on the line OC so that GP=GO.
8. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.

Solution 5
Utilizing an isosceles triangle whose sides are x:y:y in length (2) (x="the radius of the circular sector" and y="the radius plus half the chord") (cf. Solution 5 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E on the line OC so that OE=AD and CO<CE.
5. Put a point F so that CF=CE and EF=OC.
6. Draw a line segment CF. And put a point G on this so that CG=CO.
7. Put a point P on the line segment OC so that OP=OG.
8. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
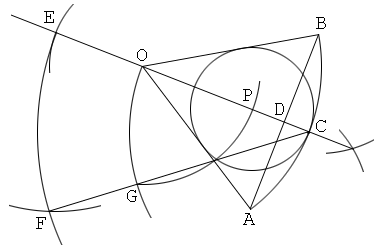
Solution 6
Determining points that are on the circumference of a circle concentric with a circle to be constructed (cf. Solution 6 of construction problem 2)
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a chord AB, and let D be the intersection of this and OC.
4. Put a point E on the line segment OC so that CE=AD.
5. Draw a line through E that is parallel to AD, and let F be the intersection of this and OA.
6. Draw a perpendicular bisector of FC, and let P the intersection of this and OC.
7. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
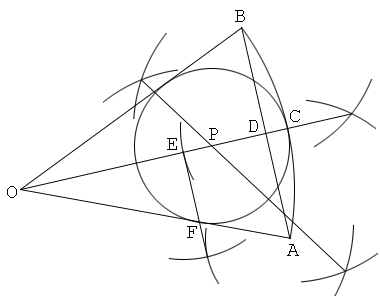
Solution 7
Determining tangent points between the circular sector and its inscribed circle
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a line through O that is perpendicular to OA. And put a point D on this so that OD=OA and DA<DB.
4. Draw a line CD and let E be the intersection of this and OA.
5. Draw a perpendicular bisector of CE, and let P the intersection of this and OC.
6. Draw a circle with its center P and its radius PE. Then the circle P is the inscribed circle of the circular sector OAB.

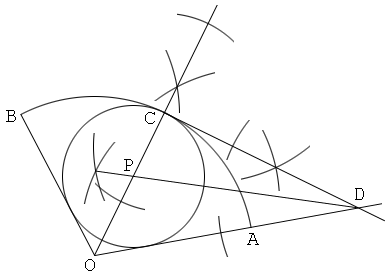
Solution 8
Constructing the inscribed circle of an isosceles triangle
1. Draw a circular sector OAB, with its center O and its arc AB.
2. Draw a bisector of the central angle O, and let C be the intersection of this and the arc AB.
3. Draw a line from C that is perpendicular to OC. And let D be the intersection of this and an extended line OA.
4. Draw a bisector of an angle ODC, and let P the intersection of this and OC.
5. Draw a circle with its center P and its radius PC. Then the circle P is the inscribed circle of the circular sector OAB.
Mathematical Problems