Construction problem 1
Construct a rectangle with compasses and a straightedge.

Hints for solutions
Solution 1: Drawing a circle and two lines that are diagonals of a rectangle
Solution 2: Drawing four circles to determine the four vertices of a rectangle
Solution 3: Drawing two pairs of concentric circles
Construction problem 2
With compasses and a straightedge, first draw a line segment, and then construct a point that divides the line segment internally in the ratio 1:2.
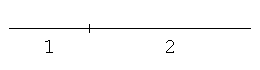
Hints for solutions
Solution 1: Constructing, a line segment that is parallel to the initial line, and a point that divides the line segment externally 2:3
Solution 2: Constructing a pair of parallel lines each of which passes through either end of the initial line segment
Solution 3: Constructing a triangle whose one side is the initial line segment, and the other sides are 1:2 in length
Solution 4: Utilizing an isosceles triangle whose sides are 2:3:3 in length (1) (An isosceles triangle of 1:3:3 can be utilized instead.)
Solution 5: Utilizing an isosceles triangle whose sides are 2:3:3 in length (2) (An isosceles triangle of 1:3:3 can be utilized instead.)
Solution 6: Determining points that are on the circumference of a circle whose center is a point to be constructed
Solution 7: Constructing an equilateral triangle and its centroid, with its one side the initial line segment
Solution 8: Utilizing that the centroid of a triangle cuts a line segment between one vertex of the triangle and the midpoint of the opposite side in the ratio 2:1
Construction problem 3
With compasses and a straightedge, first draw two line segments, and then, letting 'a' and 'b' be the lengths of them, draw a line segment whose length is √(ab).
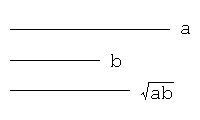
Hints for solutions
Solution 1: Utilizing (a+b)2-(a-b)2=4ab
Solution 2: Utilizing (a-b/2)2-(b/2)2=a2-ab, and a2-(a2-ab)=ab
Solution 3: Utilizing (a-b)2+b2-2(a-b)b*cos120°=a2+b2-ab, and (a2+b2-ab)-(a-b)2=ab
Solution 4: Utilizing a right triangle that is divided into two similar right triangles
Solution 5: Utilizing, a line that intersects a circle at two points, and another line that touches the circle
Construction problem 4
With compasses and a straightedge, first draw a circular sector with its central angle less than 180°, and then construct an inscribed circle of the circular sector.
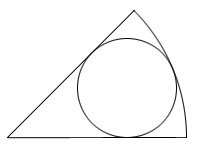
Hints for solutions
Solution 1: Constructing, a line segment that is parallel to the bisector of the central angle, and a point that divides the line segment internally in the ratio "the radius" to "half the chord" (cf. Solution 1 of construction problem 2)
Solution 2: Constructing, a line that passes through the center of the circular sector, and another line that is parallel to the line and that passes through the midpoint of the arc (cf. Solution 2 of construction problem 2)
Solution 3: Constructing a triangle whose one side is the line segment between the center of the circular sector and the midpoint of the arc, and the other two sides are "the radius" to "half the chord" in length (cf. Solution 3 of construction problem 2)
Solution 4: Utilizing an isosceles triangle whose sides are x:y:y in length (1) (x="the radius of the circular sector" and y="the radius plus half the chord") (cf. Solution 4 of construction problem 2)
Solution 5: Utilizing an isosceles triangle whose sides are x:y:y in length (2) (x="the radius of the circular sector" and y="the radius plus half the chord") (cf. Solution 5 of construction problem 2)
Solution 6: Determining points that are on the circumference of a circle concentric with a circle to be constructed (cf. Solution 6 of construction problem 2)
Solution 7: Determining tangent points between the circular sector and its inscribed circle
Solution 8: Constructing the inscribed circle of an isosceles triangle
Integer problem 1
What day of the week is today? Then, what day will it be, 230 days from today?
Hints for solutions
Solution 1: Calculating 230
Solution 2: Examining the remainders of 2, 22, 23, ... divided by 7s
Solution 3: Utilizing 230=810
Solution 4: Factorizing 230-1
Integer problem 2
What is the smallest positive integer that has just 15 factors?
(Note: 1 and the integer itself are included in the factors. For example, the number 6 has 4 factors, that are 1, 2, 3, and 6.)Hints for solutions
Solution 1: Noticing what integer has odd number of factors
Solution 2: Utilizing the relation between a factorized integer and the number of factors the integer has
Integer problem 3
What is the smallest positive integer whose remainder is 3 when divided by 7, whose remainder is 4 when divided by 9, and whose remainder is 2 when divided by 16?
Hints for solutions
Solution 1: Examining positive integers that satisfy the given conditions
Solution 2: Setting up equations from the given conditions
Integer problem 4
What are the last 4 digits of 7100?
Hints for solutions
Solution 1: Calculating the last 4 digits of 74, 78, 716, ...
Solution 2: Utilizing 72=49
Solution 3: Utilizing 74=2401
Integer problem 5
Factorize 111111111111, which is a product of 7 primes.
Hints for solutions
Solution 1: Factorizing the given integer in two ways
Solution 2: Multiplying the given integer by 9 before prime factorizing
Integer problem 6
A positive integer is represented, as 21022200 in a base 'n' system, and as 10112121 in a base n+1 system. What is the 'n', that is larger than 2, in the decimal system?
(Note: for example, the decimal number 37 means 3*10+7. 102 in the base 3 system is equivalent to 1*32+0*3+2.)Hints for solutions
Solution 1: Inspecting a 7th-degree polynomial of 'n' by taking its derivatives
Solution 2: Deriving two inequalities from an equation to limit n's range
Solution 3: Factorizing a 7th-degree polynomial of 'n'
Solution 4: Making the most of n's being an integer
Mathematical Problems