Mathematical Problems
Original Problems in Construction and Integer
Takashi Shimazaki
Being fond of mathematics, I have created some mathematical problems. Here you can see some of them that I think would be interesting for the intelligent beings on the planet. All the problems - four compass-and-straightedge constructions and six integer problems - are so concrete as to be understandable for around middle school students. But you should be required some ingenuity to work them out. Give it a try and have a wonderful time in tackling my sophisticated riddles!
I came up with various solutions to the problems, which are available on this site. You should not read them, however, before solving them on your own, if you want to better train your brain. Were you to discover other solutions, then please notify me of your find: I am looking forward to hearing from you! Other messages or inquiries are also welcomed.
Construction problems
Problem 1
Construct a rectangle with compasses and a straightedge.

Problem 2
With compasses and a straightedge, first draw a line segment, and then construct a point that divides the line segment internally in the ratio 1:2.
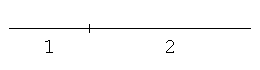
Problem 3
With compasses and a straightedge, first draw two line segments, and then, letting 'a' and 'b' be the lengths of them, draw a line segment whose length is √(ab).
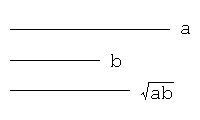
Problem 4
With compasses and a straightedge, first draw a circular sector with its central angle less than 180°, and then construct an inscribed circle of the circular sector.
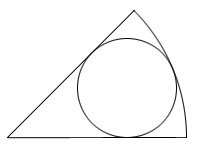
Integer problems
Problem 1
What day of the week is today? Then, what day will it be, 230 days from today?
Problem 2
What is the smallest positive integer that has just 15 factors?
(Note: 1 and the integer itself are included in the factors. For example, the number 6 has 4 factors, that are 1, 2, 3, and 6.)Problem 3
What is the smallest positive integer whose remainder is 3 when divided by 7, whose remainder is 4 when divided by 9, and whose remainder is 2 when divided by 16?
Problem 4
What are the last 4 digits of 7100?
Problem 5
Factorize 111111111111, which is a product of 7 primes.
Problem 6
A positive integer is represented, as 21022200 in a base 'n' system, and as 10112121 in a base n+1 system. What is the 'n', that is larger than 2, in the decimal system?
(Note: for example, the decimal number 37 means 3*10+7. 102 in the base 3 system is equivalent to 1*32+0*3+2.)Hints for solutions
Construction problem 1Construction problem 2
Construction problem 3
Construction problem 4
Integer problem 1
Integer problem 2
Integer problem 3
Integer problem 4
Integer problem 5
Integer problem 6
www.tadopika.net/en/
About the Author