作図問題2
コンパスと直定規を使い、初めに線分を描き、次にこの線分を1:2に内分する点を作図せよ。
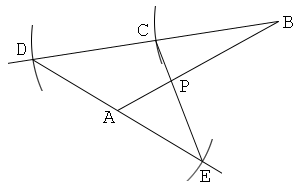
解答1
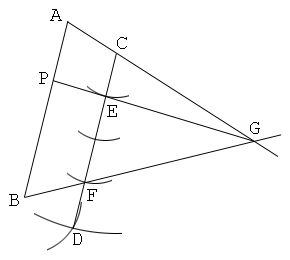
最初の線分に平行な線分と、この線分を2:3に外分する点、を作図
1. 線分ABを描く。
2. 点Cを置く。続いて、四角形ABDCが平行四辺形になるように点Dを取る。
3. 直線CDを引き、この上にCE:EF=1:2且つEF<CFとなるように点E, Fを取る。
4. 直線ACと直線BFを引き、これらの交点をGとする。
5. 直線EGを引き、これとABの交点をPとする。すると、点Pは線分ABを1:2に内分する。
解答2
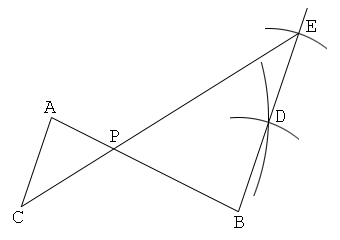
最初の線分の両端を通る二本の平行線を作図
1. 線分ABを描く。
2. 点Cを置く。続いて、四角形ACBDが平行四辺形になるように点Dを取る。
3. 直線BDを引き、この上にBD=DEとなるように点Eを取る。
4. 直線CEを引き、これとABの交点をPとする。すると、点Pは線分ABを1:2に内分する。
解答3
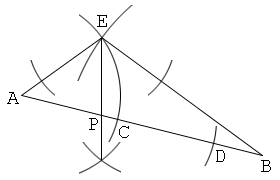
最初の線分を一辺とし、他の二辺は長さが1:2となる三角形を作図
1. 線分ABを描く。
2. 例えば直線AB上に、AC:AD=1:2となるように点C, Dを取る。
3. AE=AC, BE=ADとなるように点Eを取る。そして、直線EAと直線EBを引く。
4. 角AEBの二等分線を描き、これとABの交点をPとする。すると、点Pは線分ABを1:2に内分する。
解答4
辺の比が2:3:3である二等辺三角形を利用(1)(代わりに1:3:3の二等辺三角形を利用することもできる。)
1. 線分ABを描く。
2. 直線AB上に、BC:BD=2:3となるように点C, Dを取る。
3. CE=BE=BDとなるように点Eを取る。
4. 直線BEを引く。そして、この上にBF=BA且つAF//DEとなるように点Fを取る。
5. 直線AB上にFP=FBとなるように点Pを取る。すると、点Pは線分ABを1:2に内分する。
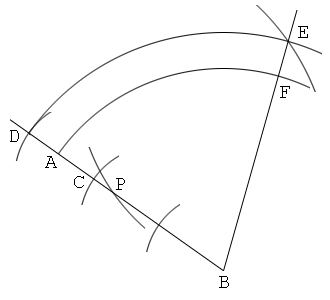
解答5
辺の比が2:3:3である二等辺三角形を利用(2)(代わりに1:3:3の二等辺三角形を利用することもできる。)
1. 線分ABを描く。
2. 直線AB上に、AC:AD=2:3となるように点C, Dを取る。
3. AE=AD且つDE=ACとなるように点Eを取る。
4. 直線AEを引く。そして、この上にAF=AB且つBF//DEとなるように点Fを取る。
5. 線分AB上にBP=BFとなるように点Pを取る。すると、点Pは線分ABを1:2に内分する。
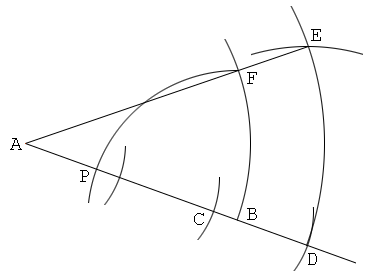
解答6
作図すべき点を中心とする円の周上の点を定める方法
1. 線分ABを描く。
2. ABの中点を作図し、これをCとする。
3. 例えば直線AB上に、CE:DE=1:2となるように点D, Eを取る。
4. CF=CE, BF=DEとなるように点Fを取る。
5. AFの垂直二等分線を描き、これとABの交点をPとする。すると、点Pは線分ABを1:2に内分する。
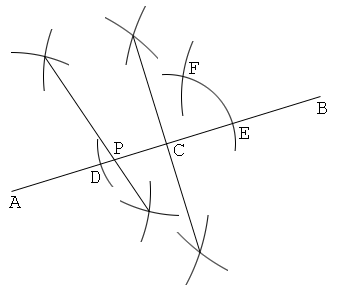
解答7
最初の線分を一辺とする正三角形、及びその重心、を作図
1. 線分ABを描く。
2. AC=BCとなる点Cを取る。
3. 正三角形ABCの重心を作図し、これをDとする。
4. ADの垂直二等分線を描き、これとABの交点をPとする。すると、点Pは線分ABを1:2に内分する。
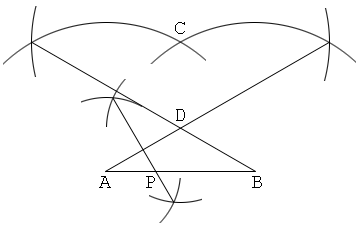
解答8
三角形の重心は「一頂点と、その対辺の中点」を2:1に内分する、ということを利用
1. 線分ABを描く。
2. Bから直線を引き、この上にBC=CDとなるように点C, Dを取る。
3. 直線DAを引き、この上にDA=AEとなるように点Eを取る。
4. 直線ECを引き、これとABの交点を点Pとする。すると、点Pは線分ABを1:2に内分する。
数学の問題