作図問題3
コンパスと直定規を使い、初めに2本の線分を描き、次に、先の線分の長さをa, bとしたとき、長さが√(ab)となる線分を作図せよ。
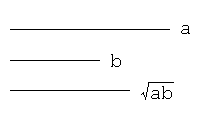
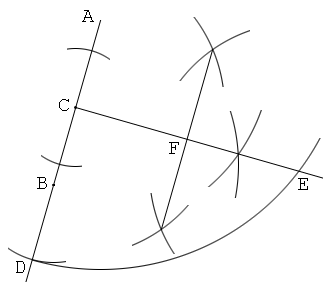
解答1
(a+b)2-(a-b)2=4abを利用
1. 線分ABを描き、この上に点Cを取る。そして、AB=a, BC=bとする。
2. ABの延長線上にBD=BCとなるように点Dを取る。
3. CからABの垂線を描き、この上にAE=ADとなるように点Eを取る。
4. CEの中点を作図し、これをFとする。すると、CF=√(ab)となる。
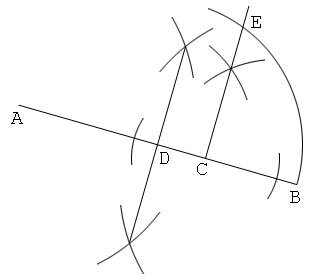
解答2
(a-b/2)2-(b/2)2=a2-ab、及びa2-(a2-ab)=abを利用
1. 線分ABを描き、この上に点Cを取る。そして、AB=a, AC=bとする。
2. ACの中点を作図し、これをDとする。更にBDの中点を作図し、これをEとする。
3. DF=DC, EF=EDとなるように点Fを取る。
4. 直線DFを引き、この上にBG=BAとなるように点Gを取る。すると、FG=√(ab)となる。

解答3
(a-b)2+b2-2(a-b)b*cos120°=a2+b2-ab、及び(a2+b2-ab)-(a-b)2=abを利用
1. 線分ABを描き、この上に点Cを取る。そして、AB=a, AC=bとする。
2. AD=CD=ACとなるように点Dを取る。
3. CからABの垂線を描き、この上にBE=BDとなるように点Eを取る。すると、CE=√(ab)となる。

解答4
互いに相似な二つの直角三角形に分割された直角三角形を利用
1. 線分ABを描き、この上に点Cを取る。そして、AC=a, BC=bとする。
2. ABの中点を作図し、これをDとする。
3. CからABの垂線を描き、この直線上にDE=DBとなるように点Eを取る。すると、CE=√(ab)となる。
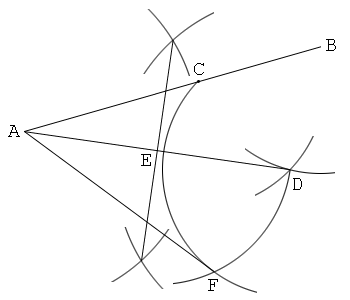
解答5
円に二点で交わる直線と、その円に接する直線、を利用
1. 線分ABを描き、この上に点Cを取る。そして、AB=a, AC=bとする。
2. BD=CDとなるように点Dを取る。
3. ADの中点を作図し、これをEとする。
4. DF=DC, EF=EDとなるように点Fを取る。そして直線AFを引く。すると、AF=√(ab)となる。
数学の問題