作図問題4
コンパスと直定規を使い、初めに中心角が180°未満の扇形を描き、次にこの扇形に内接する円を作図せよ。
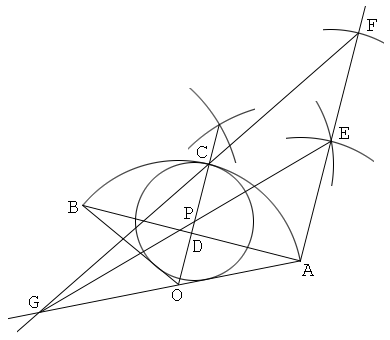
解答1
扇形の中心角の二等分線に平行な線分と、その線分を「半径」:「弦の半分」の比に内分する点、を作図(作図問題2の解答1を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 四角形OAECが菱形になるように点Eを取る。
5. 直線AEを引き、この上にEF=AD且つAE<AFとなるように点Fを取る。
6. 直線CFを引き、これとOAの延長線の交点をGとする。
7. 直線EGを引き、これとOCの交点をPとする。
8. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。
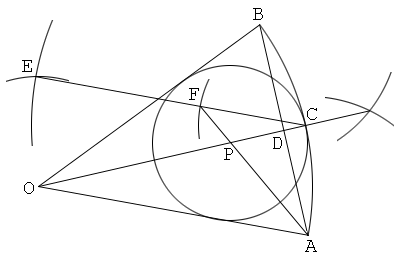
解答2
扇形の中心を通る直線と、この直線に平行で弧の中点を通る直線、を作図(作図問題2の解答2を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 四角形OACEが平行四辺形になるように点Eを取る。
5. 線分CEを引き、この上にCF=ADとなるように点Fを取る。
6. 直線AFを引き、これとOCの交点をPとする。
7. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。
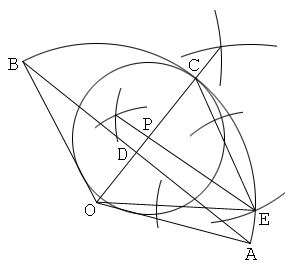
解答3
「扇形の中心と、弧の中点」を結ぶ線分を一辺とし、他の二辺は長さが「半径」:「弦の半分」となる三角形を作図(作図問題2の解答3を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 弧AC上にCE=ADとなるように点Eを取る。そして、直線EOと直線ECを引く。
5. 角OECの二等分線を描き、これとOCの交点をPとする。
6. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。
解答4
辺の比がx:y:yとなる二等辺三角形を利用(1)(x=「扇形の半径」、y=「半径」+「弦の半分」)(作図問題2の解答4を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 直線OC上にCE=AD且つOC<OEとなるように点Eを取る。
5. CF=OF=OEとなるように点Fを取る。
6. 線分OFを引く。そして、この上にOG=OCとなるように点Gを取る。
7. 直線OC上にGP=GOとなるように点Pを取る。
8. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。

解答5
辺の比がx:y:yとなる二等辺三角形を利用(2)(x=「扇形の半径」、y=「半径」+「弦の半分」)(作図問題2の解答5を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 直線OC上にOE=AD且つCO<CEとなるように点Eを取る。
5. CF=CE且つEF=OCとなるように点Fを取る。
6. 線分CFを引く。そして、この上にCG=COとなるように点Gを取る。
7. 線分OC上にOP=OGとなるように点Pを取る。
8. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。
解答6
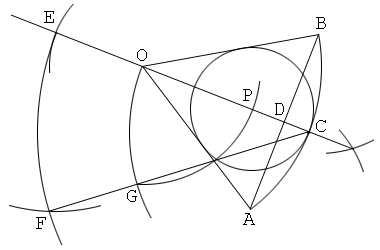
作図すべき円と同心、である円の円周上の点を定める方法(作図問題2の解答6を参照)
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. 弦ABを引き、これとOCの交点をDとする。
4. 線分OC上にCE=ADとなるように点Eを取る。
5. Eを通りADに平行な直線を描き、これとOAの交点をFとする。
6. FCの垂直二等分線を描き、これとOCの交点をPとする。
7. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。
解答7
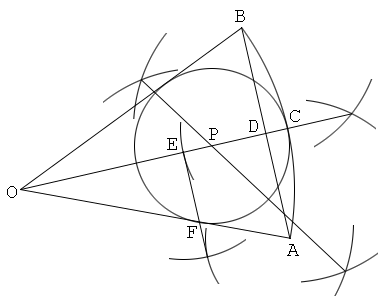
「扇形と、これに内接する円」の接点を定める方法
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. Oを通りOAに垂直な直線を描く。そして、この上にOD=OA且つDA<DBとなるように点Dを取る。
4. 直線CDを引き、これとOAの交点をEとする。
5. CEの垂直二等分線を描き、これとOCの交点をPとする。
6. 中心P、半径PEの円を描く。すると、円Pは扇形OABの内接円である。
解答8
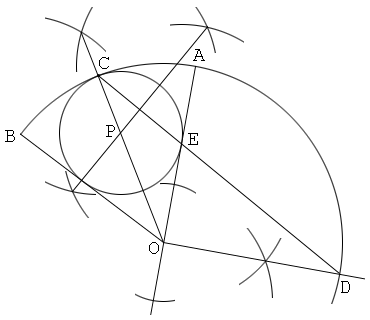
二等辺三角形の内接円を作図
1. 中心をO、弧をABとして扇形OABを描く。
2. 中心角Oの二等分線を描き、これと弧ABの交点をCとする。
3. CからOCに垂直な直線を描く。そして、これとOAの延長線の交点をDとする。
4. 角ODCの二等分線を描き、これとOCの交点をPとする。
5. 中心P、半径PCの円を描く。すると、円Pは扇形OABの内接円である。

数学の問題