作図問題1
コンパスと直定規を使い、長方形を作図せよ。

解答のヒント
解答1: 円と、長方形の対角線となる二本の直線、を描く方法
解答2: 四つの円を描いて長方形の四頂点を定める方法
解答3: 二組の同心円を描く方法
作図問題2
コンパスと直定規を使い、初めに線分を描き、次にこの線分を1:2に内分する点を作図せよ。
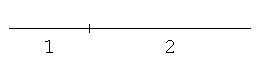
解答のヒント
解答1: 最初の線分に平行な線分と、この線分を2:3に外分する点、を作図
解答2: 最初の線分の両端を通る二本の平行線を作図
解答3: 最初の線分を一辺とし、他の二辺は長さが1:2となる三角形を作図
解答4: 辺の比が2:3:3である二等辺三角形を利用(1)(代わりに1:3:3の二等辺三角形を利用することもできる。)
解答5: 辺の比が2:3:3である二等辺三角形を利用(2)(代わりに1:3:3の二等辺三角形を利用することもできる。)
解答6: 作図すべき点を中心とする円の周上の点を定める方法
解答7: 最初の線分を一辺とする正三角形、及びその重心、を作図
解答8: 三角形の重心は「一頂点と、その対辺の中点」を2:1に内分する、ということを利用
作図問題3
コンパスと直定規を使い、初めに2本の線分を描き、次に、先の線分の長さをa, bとしたとき、長さが√(ab)となる線分を作図せよ。
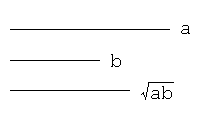
解答のヒント
解答1: (a+b)2-(a-b)2=4abを利用
解答2: (a-b/2)2-(b/2)2=a2-ab、及びa2-(a2-ab)=abを利用
解答3: (a-b)2+b2-2(a-b)b*cos120°=a2+b2-ab、及び(a2+b2-ab)-(a-b)2=abを利用
解答4: 互いに相似な二つの直角三角形に分割された直角三角形を利用
解答5: 円に二点で交わる直線と、その円に接する直線、を利用
作図問題4
コンパスと直定規を使い、初めに中心角が180°未満の扇形を描き、次にこの扇形に内接する円を作図せよ。
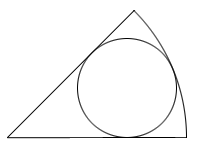
解答のヒント
解答1: 扇形の中心角の二等分線に平行な線分と、その線分を「半径」:「弦の半分」の比に内分する点、を作図(作図問題2の解答1を参照)
解答2: 扇形の中心を通る直線と、この直線に平行で弧の中点を通る直線、を作図(作図問題2の解答2を参照)
解答3: 「扇形の中心と、弧の中点」を結ぶ線分を一辺とし、他の二辺は長さが「半径」:「弦の半分」となる三角形を作図(作図問題2の解答3を参照)
解答4: 辺の比がx:y:yとなる二等辺三角形を利用(1)(x=「扇形の半径」、y=「半径」+「弦の半分」)(作図問題2の解答4を参照)
解答5: 辺の比がx:y:yとなる二等辺三角形を利用(2)(x=「扇形の半径」、y=「半径」+「弦の半分」)(作図問題2の解答5を参照)
解答6: 作図すべき円と同心、である円の円周上の点を定める方法(作図問題2の解答6を参照)
解答7: 「扇形と、これに内接する円」の接点を定める方法
解答8: 二等辺三角形の内接円を作図
整数問題1
今日は何曜日か? では、230日後は何曜日か?
解答のヒント
解答1: 230を計算
解答2: 2, 22, 23, ... を7で割ったときの余りを調べる方法
解答3: 230=810を利用
解答4: 230-1を因数分解
整数問題2
ちょうど15個の約数を持つ自然数、の中で最小のものを求めよ。
(注: 約数には、1及びその数自身を含める。例えば、6の約数は、1, 2, 3, 6の4個である。)解答のヒント
解答1: 約数の個数が奇数になるような整数を発見
解答2: 素因数分解された整数と、その約数の個数、の関係を利用
整数問題3
「7で割ると3余り、9で割ると4余り、16で割ると2余る自然数」の中で最小のものを求めよ。
解答のヒント
解答1: 与えられた条件を満たすような整数を調べる方法
解答2: 与えられた条件を式にする方法
整数問題4
7100の下4桁を求めよ。
解答のヒント
解答1: 74, 78, 716, ... の下4桁を計算していく方法
解答2: 72=49を利用
解答3: 74=2401を利用
整数問題5
111111111111は7個の素数の積である。そのように表せ。
解答のヒント
解答1: 与えられた数を二つの方法で因数分解
解答2: 与えられた数を9倍してから素因数分解
整数問題6
ある自然数は、n進法で表すと21022200となり、(n+1)進法で表すと10112121となる。nは、十進法で表すと、何か? 但し、nは2より大きい自然数とする。
(注: 例えば、十進法によると37は、3*10+7を表す。又、三進法で102は、1*32+0*3+2を意味する。)解答のヒント
解答1: nの7次多項式を、その導関数を求めて分析
解答2: 等式から二つの不等式を導き、nの範囲を限定
解答3: nの7次多項式を因数分解
解答4: nが整数であることを有効に活用
数学の問題