数学の問題
作図と整数の独創的な問題
島崎 崇
私は、数学が好きで、今までに幾つかの数学の問題を創作した。それらの中から、私が、地球上の知的生命にとって興味深いだろう、と考える問題をここに公開する。これらの問題(コンパスと直定規による作図問題が4問と整数問題が6問)は、どれも具体性の高いものなので、中学生くらいでも理解することができる。しかし、これらを解くには幾分かの創造力が要求されるだろう。気軽に私の洗練された難問に挑戦し、すてきな時を過ごしてくれ!
私はこれらの問題に対して様々な解答を編み出した。それらはこのサイトで見ることができる。しかし、より頭脳を鍛えたいのなら、問題を自力で解くまでは解答を読まない方が良い。もし私の用意した解答以外の解法を見つけた場合は、それを私に知らせてほしい(君からの連絡を楽しみにしている!)。その他の伝言や質問も歓迎する。
作図問題
問題1
コンパスと直定規を使い、長方形を作図せよ。

問題2
コンパスと直定規を使い、初めに線分を描き、次にこの線分を1:2に内分する点を作図せよ。
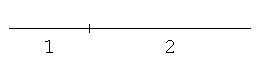
問題3
コンパスと直定規を使い、初めに2本の線分を描き、次に、先の線分の長さをa, bとしたとき、長さが√(ab)となる線分を作図せよ。
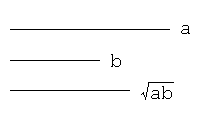
問題4
コンパスと直定規を使い、初めに中心角が180°未満の扇形を描き、次にこの扇形に内接する円を作図せよ。
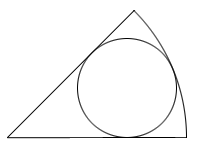
整数問題
問題1
今日は何曜日か? では、230日後は何曜日か?
問題2
ちょうど15個の約数を持つ自然数、の中で最小のものを求めよ。
(注: 約数には、1及びその数自身を含める。例えば、6の約数は、1, 2, 3, 6の4個である。)問題3
「7で割ると3余り、9で割ると4余り、16で割ると2余る自然数」の中で最小のものを求めよ。
問題4
7100の下4桁を求めよ。
問題5
111111111111は7個の素数の積である。そのように表せ。
問題6
ある自然数は、n進法で表すと21022200となり、(n+1)進法で表すと10112121となる。nは、十進法で表すと、何か? 但し、nは2より大きい自然数とする。
(注: 例えば、十進法によると37は、3*10+7を表す。又、三進法で102は、1*32+0*3+2を意味する。)解答のヒント
作図問題1作図問題2
作図問題3
作図問題4
整数問題1
整数問題2
整数問題3
整数問題4
整数問題5
整数問題6
www.tadopika.net/
著者について